

Reazione-diffusione. Da Wikipedia, l'enciclopedia libera.
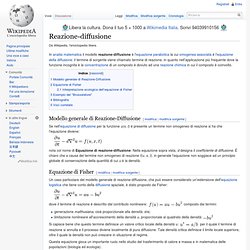
Leggi di Fick. Da Wikipedia, l'enciclopedia libera.
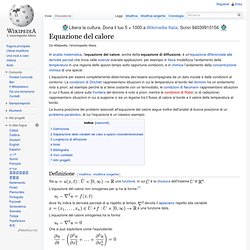
In analisi matematica, l'equazione del calore, anche detta equazione di diffusione, è un'equazione differenziale alle derivate parziali che trova nelle scienze svariate applicazioni: per esempio in fisica modellizza l'andamento della temperatura in una regione dello spazio-tempo sotto opportune condizioni, e in chimica l'andamento della concentrazione chimica di una specie. La buona posizione dei problemi associati all'equazione del calore segue inoltre dall'analisi di buona posizione di un problema parabolico, di cui l'equazione è un classico esempio. Anisotropic diffusion. In image processing and computer vision, anisotropic diffusion, also called Perona–Malik diffusion, is a technique aiming at reducing image noise without removing significant parts of the image content, typically edges, lines or other details that are important for the interpretation of the image.[1][2][3] Anisotropic diffusion resembles the process that creates a scale space, where an image generates a parameterized family of successively more and more blurred images based on a diffusion process.

Each of the resulting images in this family are given as a convolution between the image and a 2D isotropic Gaussian filter, where the width of the filter increases with the parameter. This diffusion process is a linear and space-invariant transformation of the original image. Formal definition[edit] Formally, let denote a subset of the plane and be a family of gray scale images, then anisotropic diffusion is defined as where denotes the Laplacian, denotes the gradient, is the diffusion coefficient. Reaction-Diffusion Textures. Gray-Scott reaction-diffusion java applet. How can patterns be formed by chemical reactions?

A first answer to this question was provided by Alan Turing, who specified mathematical conditions necessary for it to be possible to form spatial patterns in two-component reaction-diffusion systems. The java applet on this page simulates diffusion and reaction between two chemicals U and V. Reaction: U + 2 V -> 3 V The chemical U diffuses faster than V, and is used as fuel to produce chemical V, while chemical V catalyzes its own production. Java demo: Gray-Scott Reaction-Diffusion. Most of these images are linked to an applet with the same parameters so you can watch and interact with the pattern evolution.

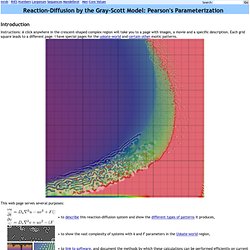
Varying F, k, and diffusion parameters Parameters: F=0.035&k=0.065&diffuseU=0.16&diffuseV=0.08& simwidth=400&simheight=400& wrap=false&varyPhysics=true& diffuseU2=0.06&diffuseV2=0.03&F2=0.06&k2=0.062 This image shows how physical parameters can vary within a single environment. Here the diffusion constants vary on the vertical axis, and the reaction constants vary along the horizontal axis.
Click the image to see these parameters in action. Reaction-Diffusion by the Gray-Scott Model: Pearson's Parameterization at MROB. Introduction Instructions: A click anywhere in the crescent-shaped complex region will take you to a page with images, a movie and a specific description.
Each grid square leads to a different page. I have special pages for the uskate-world and certain other exotic patterns. This web page serves several purposes: This work led to new discoveries and scientific investigation described below. What Is It? All of the images and animations were created by a computer calculation using the formula (two equations) shown below. Insight Into Biology The patterns created by this equation, and other very similar equations, seem to closely resemble many patterns seen in living things.
Microemulsion structure. Nervous System – explorations in generative design and natural phenomena » reaction diffusion. Nervous System has released Reaction, their first collection of housewares.
The collection includes porcelain cups and plates and matching 3D printed lamps. The pieces are intricately embossed with intertwining patterns […] Read Article → Cellular Automata – How the Leopard gets its spots. « Jonathan Pace. I’ve been reading up on how you can take a set of individual ‘things’, give each thing a rule to iterate, then sit back and watch them exhibit some interesting behaviour.

These systems are classified as ‘Cellular Automata’ ( and can be simulated in a number of different ways. One such simulation is an array of pixels in an image. By initially randomly assigning each pixel a value of 1 or 0 (corresponding to white or black) we end up with a ‘noisy’ image like this. Now come the rules. If 5 or more of your neighbours are ‘on’, then switch off. If we iterate this rule over time we get the following effect (click to regenerate).
Example | Source The pixels seemingly organise themselves into blobs of colour on a global scale – however there is no ‘global’ rule dictating this behaviour, it arises from the local rules alone. This particular example has been likened to the development of camouflage patterns in various animals. SIMULATION PICS - Virtual Laboratory for Simulation and Analysis of Propagating Interfaces. Virtual Laboratory for Simulation and Analysis of Propagating Interfaces more... Sample Numerical Simulation Snapshots Produced with VLSAπ Normalized concentration distribution during diffusion-controlled dissolution using a hybrid eXtended Finite Element-Level Set method (Adam Ghoneim, 2011) Numerical simulation of the temperature distribution in a material with Direchlet boundary conditions at the discontinuity using the eXtended Finite Element method (Adam Ghoneim, 2011) Numerical simulation of the temperature distribution and interfacial propagation during dendritic solidification in an undercooled liquid using a coupled Fixed Grid Finite Element-Cellular Automata method (Adam Ghoneim, 2011).
Alan Turing’s Patterns in Nature, and Beyond. Gierer-Meinhardt model. The Gierer-Meinhardt model.

Blending of animal colour patterns by hybridization : Nature Communications. Computer simulations Equations used for RD systems14 can be generally described as where u and v are the concentrations of hypothetical factors, f and g are the reaction kinetics and Du and Dv are the hypothetical diffusion coefficients (or their mathematical equivalents) for u and v, respectively15, 37.

The reaction rate R was introduced for convenience of parameter adjustment. The reaction kinetics and parameters used for each simulation are as follows: The linear model:14. Kondo labo. Simulation Programs (to download, just click the labyrinth pattern) reaction-diffusion simulator for windows Vista (much faster): This program calculates the original Turing's equation reaction-diffusion simulator for XP (or older OS): This program calculates the original Turing's equation reaction-diffusion simulator for XP (or older OS) :This program calculates four famous types of RD models; GM model, Schnakenberg model, GS model and oregonator. PapersPigment pattern formation by contact-dependent depolarization.Inaba M, Yamanaka H, Kondo S. Science. 2012 Feb 10;335(6069):677. In vitro imaging of pigment cells. xanthophore touches melanophore with short dendrites, which induced depolarization of melanophore.
Changing clothes easily: connexin41.8 regulates skin pattern variation.Watanabe M, Kondo S. By changing the activity of cx418(responsible gene of leopard mutation), we made variety of the skin patterns seen in wild life. Nat Genet. 2012 Feb 19;44(3):348-51. doi: 10.1038/ng.1090.