

Qu’est ce qu’une fractale ? – Kezako. Maths En Scène / Maths et nature (Partie 1) Une branche récente des mathématiques, l’exemple de la Géométrie fractale par Jean François Colonna. 3 vérités sur les fractales, ces figures géométriques fascinantes. Les fractales - Micmaths. "Focus sur la géométrie fractale" par Jean François Colonna. Fractales niveau lycée (en anglais) FRACTALES, POINTS FIXES ET COQUILLAGES. Par Valentin Seigneur Le 3 septembre 2015 - Ecrit par Marie Lhuissier Cet article a été écrit en partenariat avec La Maison des Mathématiques et de l’Informatique.

Fractales print. Fractals. LE POUMON, UNE FRACTALE QUASI-OPTIMALE. Le 2 décembre 2013 - Ecrit par Un jour une brève Cet article a été écrit en partenariat avec Mathématique de la planète Terre Le site Mathématiques de la Planète Terre (MPT), aujourd’hui Brèves de maths, a proposé, durant toute l’année 2013, une brève quotidienne avec « pour objectif d’illustrer la variété des problèmes scientifiques dans lesquels la recherche mathématique actuelle joue un rôle important, ainsi que certains grands moments dans l’histoire des sciences où les mathématiques ont, en interaction avec les autres sciences, aidé à comprendre ce que nul n’avait compris jusque-là. » Vous pourrez retrouver la plupart de ces brèves dans notre dossier Mathématiques de la Planète Terre et l’intégralité ainsi que de nouvelles brèves, sur le site Brèves de maths.
Chez l’homme, l’oxygène, qui est le comburant de la vie, est apporté jusqu’aux cellules par le sang. Pour lire la suite Post-scriptum : Brève rédigée par Marcel Filoche (Ecole Polytechnique, CNRS) d’après les travaux de E.R. B. Fractales et médecine. Etude de la morphométrie des arbres par combinaison. Etude de la morphométrie des arbres par combinaison de la géométrie fractale et de la physique statistique J.
Duchesne 1, P. Raimbault 2 and C. Les bactéries fractales. Avant de revenir vers la physique, je fais une halte en chemin, avec un petit billet situé au point triple Art-Microbiologie-Mathématiques, consacré aux colonies de bactéries qui forment des figures fractales : comment diable ces organismes parviennent-ils à produire des structures si élaborées ?
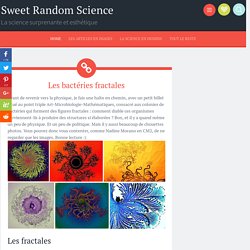
Bon, et il y a quand même un peu de physique. Et un peu de politique. Mais il y aussi beaucoup de chouettes photos. Fractales et écologie c29 Loodts.htm. Le Courrier de l'environnement n°28, août 1996 par Benoît Loodts 52, rue Salinas, 5380 Noville-les-Boil (Belgique) " Les voies sont multiples, mais la " voie est unique " Yi-King Cette fin de siècle aura consacré, dans une grande majorité des disciplines scientifiques, un revirement épistémologique d'importance, voire un changement radical de paradigme : d'analytique aux temps du scientisme, elle tend au syncrétisme, à l'approche holistique des phénomènes étudiés.

Bien sûr cette tendance existe implicitement depuis la naissance du discours scientifique et s'est exprimée à quelques reprises. 51 Une foret fractale. Résumé : en partant de la relation d’Euler et en manipulant des nombres complexes, on peut produire des images fractales très belles qui rappellent des forêts.

Mots-clés : nombre complexe, relation d’Euler, fractal. L'inventeur des antennes Fractales. Antenna Theory: Fractal Facts. Carles Puente & team - Fractal-based antennae for mobile phones. Carles Puente, Carmen Borja, Jaume Anguera, Jordi Soler Castany, Edouard Rozan (Spain) Invention: Fractal-based antennae for mobile phones Today’s mobile devices allow users across the globe to communicate on-the-go and connect to the Internet.
The compact size of these gadgets is made possible by tiny, highly powerful antennae based on the principles of fractal geometry. Invented by Catalan engineer Carles Puente Baliarda, fractal-based antennae have put global communications into the hands of millions. In 1995, Carles Puente Baliarda and his team invented the world’s first fractal-based antenna for mobile communication. The antennae derive their name – and powerful broadcast abilities – from geometrical properties: Fractals are patterns consisting of multiple small copies of themselves, which allows for “coiling” long antennae into the small confines of mobile devices.
Conventional antennae, such as the ones used in FM broadcast, require a certain length in order to broadcast and receive signals at full capacity; about 1.5 metres for a standard radio antenna. Analog Fractals with 1930's Technology. Marble Marcher - A Fractal Physics Game. The Hardest Mandelbrot Zoom Ever In 2014,10^198 : New record - 350 000 000 iterations. Où trouve-t-on des fractales ? - Site sur les nombres complexe et les Fractales. Au IVe siècle avant J.-C. : Euclide définit la notion de dimension entière - Site sur les nombres complexe et les Fractales. Master_Thesis_Lajoie.pdf Document Adobe Acrobat 4.7 MB Voici les grandes étapes pour que les fractales puissent apparaître et se développer : D1.
La notion expérimentale la plus simple est celle de "volume". Les fractales, une géométrie "complexe" incontournable ! - Site sur les nombres complexe et les Fractales. Kézako : qu'est-ce qu'une fractale ? Les fractales, ces structures géométriques qui se répètent à l'infini, ont de quoi réconcilier tout un chacun avec les mathématiques.
Mais elles sont aussi hypnotisantes que complexes. Pour explorer en toute sérénité la dimension fractale, Unisciel et l'université de Lille 1 nous offrent cet épisode de Kézako. Les fractales sont des objets mathématiques particulièrement complexes, qui ne s'expliquent pas par la géométrie conventionnelle. Elles présentent une structure invariante par changement d'échelle : on retrouve des détails identiques, ou similaires, quand on zoome à l'infini. Par ailleurs, ces objets ont une dimension fractale, en général non entière.
Bio-inspirations, fractales, complexité et émergence. Mieux mettre l'informatique au service des problèmes humains. S'inspirer de la biologie : la biocomplexité, les phénomènes d'émergence. Lorsque l'on conçoit des systèmes artificiels à grande échelle, on produit souvent des comportements macroscopiques irréguliers, sur lesquels on constate que l'on a peu de contrôle.
Parallèlement, les applications bio-informatiques ont drainé l'attention des chercheurs sur la complexité des systèmes biologiques (sociétés d'insectes, modèles de croissance fractale), pour lesquels cette caractéristique est un atout, en robustesse et capacité d'adaptation, notamment. Algorithmes évolutionnaires. L'une des approches de la complexité abordée au projet Fractales est fondée sur les algorithmes évolutionnaires. Ces techniques sont connues essentiellement pour leur potentiel en tant que méthode d'optimisation stochastique, et représentent la transposition informatique de la théorie de l'évolution selon Darwin. Le terme algorithme évolutionnaire correspond à l'ensemble des techniques fondées sur ce modèle biologique, dont les plus connues sont les algorithmes génétiques, mais on parle aussi dans ce cadre de programmation génétique, de stratégies d'évolution, de programmation évolutionnaire, selon la façon dont on traduit les principes darwiniens dans le modèle artificiel.
Le principe de base est de copier le comportement de populations d'êtres vivants, qui s'adaptent à leur environnement à l'aide de phénomènes comme la sélection naturelle, et l'héritage génétique. Fractales, multifractales. Née de l'analyse d'objets mathématiques « étranges » (comme des courbes de longueur infinie occupant une surface finie, ou des fonctions continues nulle part dérivables) à la fin du XIXe siècle, la géométrie fractale a pris son essor grâce aux travaux de Benoît Mandelbrot au milieu du XXe siècle. L'argument étant que ces curiosités mathématiques étaient en fait des objets que l'on retrouve assez couramment dans la nature. 15 images fractales renversantes. Darwin et les fractales. Ce sont précisément ces outils fractals de modélisation de l'irrégularité qui sont pertinents pour affiner l'analyse d'un modèle darwinien artificiel simple. Cette approche vient à point pour consolider les intuitions que l'on peut avoir sur ces méthodes évolutionnaires : en d'autres termes, des constatations comme par exemple « plus les fonctions sont irrégulières, plus il est difficile de localiser un optimum global ».
Toutefois l'outil fractal permet d'aller au-delà d'une qualification empirique. Bon nombre de questions théoriques s'ouvrent alors, et notamment concernant le grand problème de l'analyse des vitesses de convergence et de la qualité des solutions. D'un autre côté, Darwin peut être lui aussi utile aux fractalistes. Pour finir avec un exemple artistique de Darwinisme artificiel appliqué à un problème fractal, toutes les images artificielles que vous pouvez voir dans cette page ont été créées avec le logiciel ArtiE-Fract. Quel est la longueur du périmètre de la France ? (solution) — lesenfantcodaient.fr. Les fractales Le périmètre de la France est infini mais sa surface l’est. C’était la conclusion de la petite digression que je me suis permis lors du dernier coding gouter. Si on le laisse de côté le phénomène des marées qui complique un peu les choses, il est assez facile de parcourir le bord de France avec des tiges d’une longueur d’un kilomètre pour entourer maladroitement le pays.
Et si maintenant, on cassait une tige 10 en petits bouts de 100 mètres pour aller au plus près de la côte. Il nous manquerait un peu de longueur pour finir. IFS, fractales et jeu du chaos. Y. Morel Des images et des fractales. Physique et Structures Fractales. 90 Le baiser infini. Suites de farey 2014. Top 8 des monstres mathématiques. Newton's Fractal (which Newton knew nothing about) Fractales "algorithmiques" Fractales.
Tour de Hanoï. Les ensembles de Mandelbrot - JM Alliot. Mandelbrot en Python. Orbit of zero for Mandelbrot-To visualize the Mandelbrot set. Master Thesis Lajoie. PYTHAGORE ET LES COURBES DE PÓLYA. Le théorème de Pythagore est enseigné dans les collèges français. Fractales.