

6-034-fall-2010. TIPE 2016-2017 Optimalité : choix, contraintes, hasard. Optimisation et apprentissage : Alexandre d'Aspremont, 2014. Convexité et optimisation : cours de Guy Cohen, 2000, corr. 2006. Les mathématiques, la clé d'un trafic fluide ? - 31/07/2015 - ladepeche.fr. Si vous prenez la route ce week-end à l'occasion du grand chassé-croisé de l'été et que les centaines de kilomètres de bouchons attendus vous angoissent, rassurez-vous: des mathématiciens tentent d’alléger vos souffrances en définissant des systèmes de régulation du trafic.
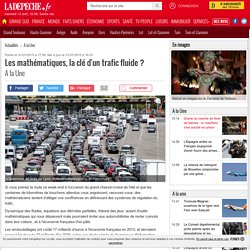
Dynamique des fluides, équations aux dérivées partielles, théorie des jeux: autant d'outils mathématiques qui nous dépassent mais pourraient éviter aux automobilistes de rester coincés dans leur voiture...et à l'économie française d'en pâtir. Les embouteillages ont coûté 17 milliards d’euros à l'économie française en 2013, et devraient peser à hauteur de 22 milliards d'ici 2030, selon une étude signée du fournisseur d'information routière INRIX et du Centre for Economics and Business Research (Cebr).
Soit plus que le trou de la Sécu en 2014. "J'étudie des équations qui décrivent l'écoulement d'un gaz ou d'un fluide", explique-t-elle à l'AFP. Dossier thématique sur transport optimal dans Images des mathématiques. Le prix de l'anarchie ou le paradoxe de Braess, Étienne Ghys, 2009. Deux paradoxes Pour expliquer cela, nous allons commencer par décrire un autre phénomène découvert par A.C.

Pigou — un économiste — en 1920 [2]. Supposons que deux villes et , de part et d’autre d’un fleuve, soient reliées par deux routes. La première est excellente, très large, mais elle fait malheureusement un grand détour : il faut une heure pour la parcourir, et ceci quel que soit le nombre de véhicules qui l’empruntent (dans des limites raisonnables, par exemple jusqu’à 1000 véhicules par heure). La seconde passe par un pont très étroit et très court, et on peut le parcourir en quelques instants à peine, à condition d’être seul sur le pont. John Nash, la théorie des jeux et la question du bon choix : article du Monde, mai 2013.
Le mathématicien et prix Nobel John Forbes Nash est mort à l'âge de 86 ans.
L'occasion de revenir sur sa spécialité, la théorie des jeux. LE MONDE SCIENCE ET TECHNO | • Mis à jour le | Philippe Pajot Le mathématicien américain John Forbes Nash est mort à l'âge de 86 ans. Ci-dessous, un article datant de mai 2013 où il est question de sa spécialité, la théorie des jeux. « Gouverner, c'est choisir », disait Pierre Mendès France. «Optimalité : choix, contraintes, hasard.» un thème où l’on retrouve la déraisonnable efficacité des mathématiques grâce à l’informatique. — Pixees. Trois mots clés qui se fédèrent en une théorie.

©IHP – Maison des mathématiques. Les mathématiques se mettent au service de problèmes concrets pour produire grâce à l’informatique, les meilleures solutions.