

Acoustic resonance. Acoustic resonance. Sound waves scale. Sound waves. Electromagnetic radiation. Sound waves. Lattice Vibrations. Acoustical phonons. Lets consider a linear chain of identical atoms of mass M spaced at a distance , the lattice constant, connected by invisible Hook's law springs.

For simplicity we will consider longitudinal deformations - that is, displacements of atoms are parallel to the chain. Let Un =displacement of atom n from its equilibrium position Un-1=displacement of atom n-1 from its equilibrium position Un+1=displacement of atom n+1 from its equilibrium position The force on atom n will be given by its displacement and the displacement of its nearest neighbors : The equation of motion is: where is a spring constant. The above equation is not obviously a wave equation, but let us assume a traveling wave solution, namely, Let Uno = Uo since if it is a wave, it has to have a definite amplitude. If we substitute our wave solution into equation of motion we find a phonon's dispersion relation for linear monatomic chain as follows: The dispersion curve is shown below. , the repeat period is and we have.
Lattice Vibrations. Article about Lattice Vibrations by The Free Dictionary. One of the main types of internal motion of a solid, in which the constituent particles (atoms or molecules) oscillate about equilibrium positions—the lattice points.
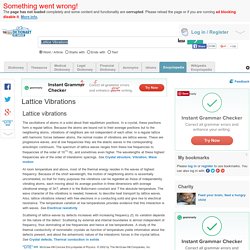
For example, lattice vibrations in the form of standing or traveling sound waves arise whenever a crystal is acted upon by an external force that varies over time. However, even in the absence of external influences a steady state of vibrations is established in a crystal that is in thermal equilibrium with its environment, just as a fixed distribution of atoms or molecules is established in a gas according to their rate of translatory motion.
What is it about metal, molecularly, that makes it clink or ring when struck? Do these chemical characteristics define metal or does all metal simply happen to have these characteristics? - Quora. Primary Metallic Crystalline Structures. Primary Metallic Crystalline Structures (BCC, FCC, HCP) As pointed out on the previous page, there are 14 different types of crystal unit cell structures or lattices are found in nature.
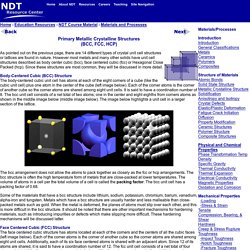
However most metals and many other solids have unit cell structures described as body center cubic (bcc), face centered cubic (fcc) or Hexagonal Close Packed (hcp). Since these structures are most common, they will be discussed in more detail. Body-Centered Cubic (BCC) Structure The body-centered cubic unit cell has atoms at each of the eight corners of a cube (like the cubic unit cell) plus one atom in the center of the cube (left image below). Each of the corner atoms is the corner of another cube so the corner atoms are shared among eight unit cells.
The bcc arrangement does not allow the atoms to pack together as closely as the fcc or hcp arrangements. Some of the materials that have a bcc structure include lithium, sodium, potassium, chromium, barium, vanadium, alpha-iron and tungsten. Waves - What characterizes a metallic sound, and why do metals have a metallic sound? Interestingly something sounding metallic has its origin in its dimensions rather than the material, and this effect is only amplified by the material.
The character of perceived sound is mostly determined by the excited oscillations of an object, the so called modal structure. The modes of an object depend on the geometry. An approximately one-dimensional object like a long thin cylinder will have mode frequencies that come as integer multiples of a fundamental frequency. These can be easily grouped by our auditory cortex to result in a single tonal perception with a timbral character depending on the energy distribution in the vibrational modes. We call this frequency structure "harmonic". A 2 or 3 dimensional object has additional frequencies that cannot be described as harmonic overtones of a fundamental. If there is no good harmonic approximation and a lot of modes are excited with high energy then the sound is not tonal anymore.
Speed of Sound in some common Solids. Speed of sound in some common solids like aluminum, brass, concrete and ...

Speed of sound in normal air is 343 m/s. In water the speed of sound is 1433 m/s. Sound velocity in some common solids are indicated in the table below: 1 m/s = 3.6 km/h = 196.85 ft/min = 3.28 ft/s = 2.237 mph Related Topics Acoustics - Room acoustics and acoustic properties - decibel A, B and C - Noise Rating (NR) curves, sound transmission, sound pressure, sound intensity and sound attenuation Related Documents Tag Search en: sound speed velocity solidses: sólidos velocidad de la velocidad del sonidode: Schallgeschwindigkeit Geschwindigkeitsfeststoffe.
Acoustic levitation.