

Mesure du 1er mètre : une erreur qui changea le monde - Omniscie... Pendant la période agitée de la révolution française deux scientifiques, Méchain et Delambre, furent chargés par le gouvernement révolutionnaire de mesurer la circonférence de la Terre.
A partir de cette mesure universelle, les scientifiques ont défini la base du système métrique aujourd’hui utilisé par plus de 95 % de la population mondiale. L’histoire de cette aventure scientifique de sept ans ponctuée d’évènements tragiques montre que la ténacité, la confiance en soi et les erreurs sont des paramètres souvent ignorés mais qui contribuent aussi à l’établissement des connaissances scientifiques. Il y a quelques années, Ken Alder, professeur d’histoire des sciences à l’université de Northwestern près de Chicago, a retrouvé les notes écrites de ces deux scientifiques français. Ces manuscrits présumés disparus depuis longtemps se trouvaient pour l’un dans les archives de l’Observatoire de Paris, pour l’autre dans une bibliothèque de l’état de l’Utah aux Etats-Unis. A la recherche des longitudes - Brèves de Maths. Le chronomètre de Harrison Au XVIIème siècle, alors que la navigation vers les Indes orientales et occidentales se développe et que l’exploration du Pacifique commence, le besoin de se repérer en pleine mer devient crucial : des explorateurs découvrent des terres, mais personne n’arrive ensuite à les retrouver !
La solution couramment utilisée actuellement consiste à déterminer sa latitude (la distance à l’équateur) et sa longitude (la distance à un méridien donné). Mesurer la latitude est aisé : on repère au sextant la hauteur de l’étoile Polaire sur l’horizon. Des triangles pour vérifier la gravitation universelle - Brèves de Maths.
Mesure de distance par triangulation.
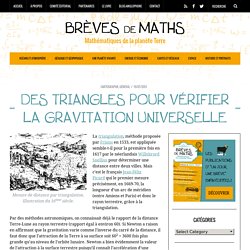
Illustration du 16ème siècle. La triangulation, méthode proposée par Frisius en 1533, est appliquée semble-t-il pour la première fois en 1617 par le néerlandais Willebrord Snellius pour déterminer une distance entre deux villes. Mais c’est le français Jean-Félix Picard qui le premier mesure précisément, en 1669-70, la longueur d’un arc de méridien (entre Amiens et Paris) et donc le rayon terrestre, grâce à la triangulation. Des triangles pour se repérer sur Terre - Brèves de Maths. Gemma Frisius, peint par Maarten van Heemskerck.
Qui connaît le nom de Gemma Frisius (1508-1555), professeur néerlandais de mathématiques ? Et pourtant son traité Libellus de Locorum describendorum ratione (1533) a une influence considérable sur nos connaissances scientifiques. Il contient en effet le plus ancien exposé connu du principe de triangulation. Cette méthode repose sur une idée simple mais extrêmement fertile : il est beaucoup plus facile de mesurer des angles que des distances. Pour déterminer la géométrie d’un territoire, on commence par découper celui-ci en triangles de façon à ce que depuis les sommets, choisis en hauteur, on puisse voir d’autres sommets (en terrain plat on se met en recherche de clochers ou de tours de châteaux bien placés).
Longitude : une histoire. Le problème de la mesure de la longitude est un enjeu crucial pour les géographes.

Pendant plus de 16 siècles, ce problème a fait l'objet de bien des recherches. Ptolémée est le premier géographe moderne. Au IIème siècle après J.C., il recense plus de 8 000 noms de lieux connus sur une carte, en fonction de leur latitude et de leur longitude. Si il est facile de connaître la latitude en mesurant les angles de l'ombre portée, le calcul des longitudes donna lieu à d'énormes erreurs d'échelle. Le Moyen Age connaît une régression scientifique majeure. Terre. Eratosthene. Objectifs de connaissance : le mouvement apparent du Soleil, lumière et ombre, la rotation de la terre sur elle-même et ses conséquences, la durée du jour et son évolution au cours des saisons.

En mathématiques : utiliser des instruments de mesure, exprimer le résultat d'un mesurage par un nombre, estimer une mesure, construire un instrument de mesure,la mesure de durées, les angles. Matériel Pour la classe : des équerres, des rapporteurs, des boussoles, du carton, ficelle, fil à plomb...... Par groupe d'élève : en fonction des expériences. Le mot du maître : voir annexe Ce projet fait partie d'une activité en astronomie menée tout au long de l'année, voir le document "Terre/Lune/Soleil". Séquence N°1. Mesurl1. Faire le « Point » Faire le " Point " Les méthodes décrites dans la littérature sont quelquefois difficiles à comprendre et à appliquer précisément.

Elles concernent plus particulièrement le marin, quelquefois le navigateur aérien, plus rarement le terrien. Première constatation : si les premiers ont un horizon bien défini, référence de toutes les mesures de " hauteur " angulaire du soleil ou des étoiles, il n’en est rien du petit citadin et dans beaucoup d’endroits au relief tourmenté du terrien en général.
En contrepartie, le sol est généralement plus stable que la mer ou les airs et surtout l’observateur conserve la même position aussi longtemps qu’il le souhaite alors que les navigateurs, par nature, voyagent entre deux mesures! Nous nous attacherons donc à décrire des méthodes permettant de trouver la position d’un lieu terrestre essentiellement fondée sur les positions occupées par le soleil dans la journée.