

Heighway Dragon. Typesetting math: 16% Classic Iterated Function Systems <p style="margin-left:20%; margin-top:10px"><b>Note</b>: This site uses Javascript.
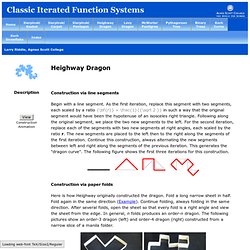
It also uses <a href=" target="_blank">MathJax</a> (which requires Javascript) to display mathematical expressions. Please turn on JavaScript, then refresh the page. </p> Description ConstructionAnimation Construction via line segments Begin with a line segment. Construction via paper folds Here is how Heighway originally constructed the dragon. ConstructionAnimation Construction via triangles For yet another way to construct the Heighway dragon, start with an isosceles right triangle H0.
The Heighway dragon is the limiting set of this iterative construction. IteratedFunctionSystem To think of this construction as a result of affine transformations, consider the first iteration of the line segment from (0,0) to (1,0) as shown by the two red line segments in the following figure. IFSAnimation where {\bf{r}} = \frac{1}{{\sqrt 2 }}. [Enlarge] L-System. Knot theory. In this Section we will cover the following aspects: Table of contents 1.Motivation ?

2.Basic knot theory ? 2.1.What is a mathematical knot? ? 2.2.Equivalence/deformation of knots ? 2.4.Diagrams of knots and links ? 2.5.3.Amphicheiral knots ? 2.5.4.Alternating knots ? 3.Advanced knot theory ? 3.1.Reidemeister moves and Reidemeister theorem ? 3.2.Invariants of knots and links ? 3.2.1.numeric invariants: unknotting number and crossing number ? 3.2.3.polynomial invariants ? 3.3.Tabulation of knots and links ?
4.Modern aspects of knot theory ? 5.References on knot theory that I find useful ? 1.Motivation My current research refers to the subject of my PhD Thesis, focused on "Symbolic numeric algorithms for genus computation of plane complex algebraic curves based on knot theory". To give a basic summary of the most important aspects of knot theory which we use for the work of the current project; to show how knot theory can be analyzed from other important significant domains of mathematics; A knot or. 9 40 - Knot Atlas.
Minimal Surfaces. Riemann sphere. The Riemann sphere can be visualized as the complex number plane wrapped around a sphere (by some form of stereographic projection – details are given below).
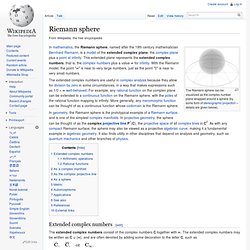
In mathematics, the Riemann sphere, named after the 19th century mathematician Bernhard Riemann, is a model of the extended complex plane, the complex plane plus a point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value ∞ for infinity. With the Riemann model, the point "∞" is near to very large numbers, just as the point "0" is near to very small numbers. In geometry, the Riemann sphere is the prototypical example of a Riemann surface, and is one of the simplest complex manifolds.
In projective geometry, the sphere can be thought of as the complex projective line P1(C), the projective space of all complex lines in C2. Extended complex numbers[edit] The extended complex numbers consist of the complex numbers C together with ∞. Arithmetic operations[edit] Metric[edit] The Scientific Graphics Project.