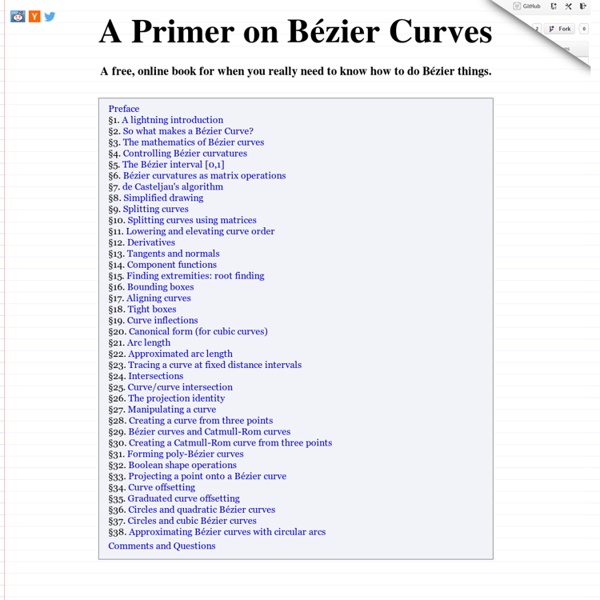
Bezier curves - a primer
Ruby on Rails Tutorial: Learn Rails by Example book and screencasts by Michael Hartl
Pixel Shaders: An Interactive Introduction to Graphics Programming
[Site] 99 Bottles of Beer
Aerotwist - Getting Started with Three.js
## Introduction I have used Three.js for some of my experiments, and it does a really great job of abstracting away the headaches of getting going with 3D in the browser. With it you can create cameras, objects, lights, materials and more, and you have a choice of renderer, which means you can decide if you want your scene to be drawn using HTML 5’s canvas, WebGL or SVG. And since it’s open source you could even get involved with the project. But right now I’ll focus on what I’ve learned by playing with it as an engine, and talk you through some of the basics. For all the awesomeness of Three.js, there can be times where you might struggle. The basics I will assume that you have at least a passing knowledge of 3D, and reasonable proficiency with JavaScript. In our 3D world we will have some of the following, which I will guide you through the process of creating: A scene A renderer A camera An object or two (with materials) Support Just a quick note on support in the browsers. Set the Scene
Python Programming Language -- Official Website
Inline
Inline is an esoteric programming language created by OberoN. Description[edit] Every value is 8-bit long and has a suffix: :b for binaries, :h for hexadecimal, :d for decimal and :a for ASCIIs. :r and :m for indexed addressing is also possible, like [0:h:r] is the address pointed by register 0 and [0:h:m] is the address pointed by memory cell 0. You can write [0-1:h:r] which is the address pointed by 0 and 1 registers, treating 0 as high part and 1 as low, and also [0-1-2:h:r] and such. In Inline immediate values are closed in parentheses. All other numbers are treated as registers. Every line is treated as a subroutine/labeled code. List of commands[edit] IO[edit] ! Inputs a char in ASCII to the memory. *(s) position Outputs a char in ASCII from the position (register or memory). " position Outputs a number from the position (register or memory). Memory[edit] register > memory Transfers the register into the memory. register < memory Transfers the memory into the register. register <> memory @ label
MiniUSPL
Still adding instructions. --OberoN 17:40, 6 November 2011 (UTC) miniUSPL (mini Unic Stack Programming Language) is an esolang. It's also a Turing tarpit. In miniUSPL you have a FIFO stack of characters, and 14 instructions, as well as 14 symbols. These are: = -> Prints the stack[0] as a char $ -> Prints the stack[0] as an int + -> stack[0]=(stack[0]+stack[1]) mod 256 - -> stack[0]=(stack[0]-stack[1]) mod 256 * -> stack[0]=(stack[0]*stack[1]) mod 256 / -> stack[0]=(stack[0]/stack[1]) mod 256 & -> stack[0]=stack[0]&stack[1] | -> stack[0]=stack[0]|stack[1] ^ -> stack[0]=stack[0]^stack[1] > -> Pushes the next char onto the stack < -> Pulls and discards the first item % -> Duplicates and pushes stack[0] onto the stack ( -> While stack[0] isn't equal to the next char, it loops over the 2nd next char { -> Start of an infinite loop } -> End of an infinite loop Programs[edit] This is the Hello World program: >H=>e=>l==>o=> =>W=o>=r>=l>=d>=>! And this calculates the Fibonacci sequence:
Related:
Related:



