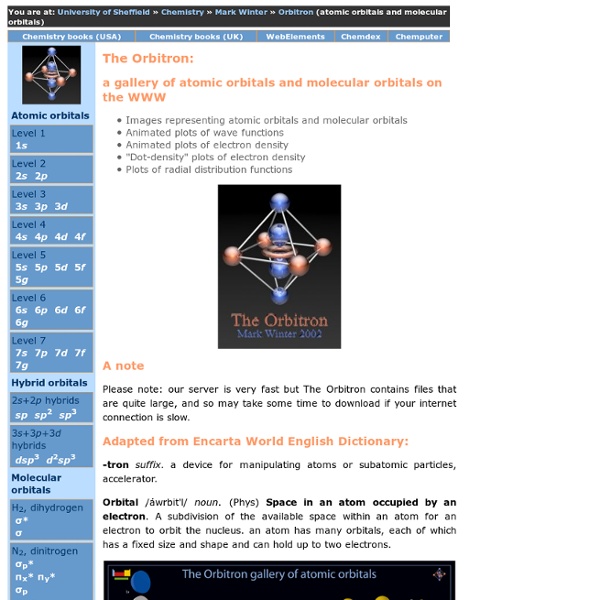
Symmetry @ Otterbein
Chemdex | The Sheffield Chemdex: the directory of chemistry on the WWW since 1993
Electron degeneracy pressure
When electrons are squeezed too close together, the exclusion principle requires them to have different energy levels. To add another electron to a given volume requires raising an electron's energy level to make room, and this requirement for energy to compress the material manifests as a pressure. Electron degeneracy pressure in a material can be computed as[4] where is the reduced Planck constant, is the mass of the electron, and is the free electron density (the number of free electrons per unit volume). This is derived from the energy of each electron with wave number , having , and every possible momentum state of an electron within this volume up to the Fermi energy being occupied. This degeneracy pressure is omnipresent and is in addition to the normal gas pressure . ) is high enough, and the temperature low enough, that the sum is dominated by the degeneracy pressure. See also[edit] References[edit] Jump up ^ Dyson, F.
ChemSpider | The free chemical database
WebElements Periodic Table of the Elements
Fermionic field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi–Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields. Basic properties[edit] Free (non-interacting) fermionic fields obey canonical anticommutation relations, i.e., involve the anticommutators {a,b} = ab + ba rather than the commutators [a,b] = ab − ba of bosonic or standard quantum mechanics. It is these anticommutation relations that imply Fermi–Dirac statistics for the field quanta. Dirac fields[edit] The prominent example of a spin-1/2 fermion field is the Dirac field (named after Paul Dirac), and denoted by ψ(x). where γμ are gamma matrices and m is the mass. and . The a and b labels are spinor indices and the s indices represent spin labels and so for the electron, a spin 1/2 particle, s = +1/2 or s=−1/2. are operators. obey the anticommutation relations: . clear. See also[edit]
JSDraw
JSDraw brings chemistry capabilities to your web pages. With this javascript libary you can display and draw chemical structures in web pages, which works cross browser, including IE, Firefox, Safari, Opera and Chrome, crose platform, including Window, Mac, Linux, and even iPhone, Android and other mobile devices. Example 2 (Editor, using molfile): Example 3 (Editor, using JSDraw compatible html): Example 4 (SDF Viewer):
David Tong -- Cambridge Lecture Notes on Quantum Field Theory
These lecture notes are based on an introductory course on quantum field theory, aimed at Part III (i.e. masters level) students. The full set of lecture notes can be downloaded here, together with videos of the course when it was repeated at the Perimeter Institute. Individual sections can be downloaded below. Last updated October 2012. PostScript PDF Videos 0. Philip Tanedo, who took this course long ago, has put together a useful literature review of quantum field theory textbooks. The late Sidney Coleman taught the quantum field theory course at Harvard for many years, influencing a generation of physicists in the way they view and teach QFT. Part 1 Part 2 These notes were subsequently latexed and posted on the arXiv. Another, older legendary QFT course was given in 1951 by Freeman Dyson.