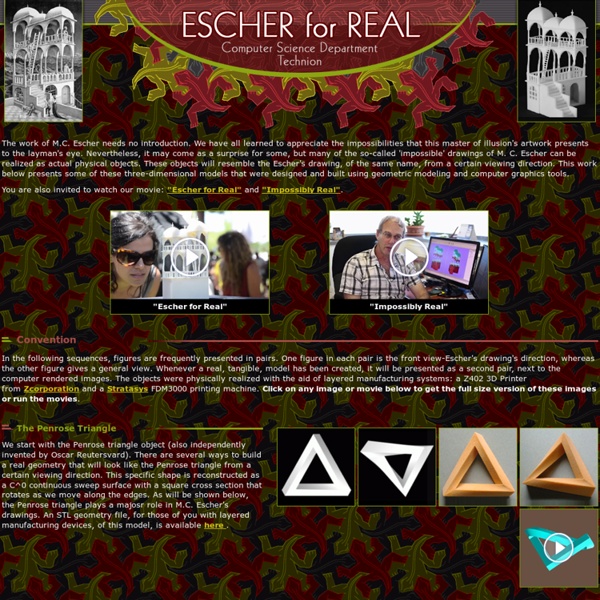
Inconsistent Images | Inconsistent Images
Impossible pictures are so-named not because the two-dimensional picture itself is impossible (for then there would be no picture!), but because what is depicted, an apparently three-dimensional thing, is impossible. This raises a significant puzzle: how can it be that one is able to draw a picture of a thing which cannot exist because to do so would violate the laws of logic or mathematics? One surely cannot draw a picture of a standard contradiction, such as "Snow is white and snow is not white." But impossible pictures are different: there is an experience "I see it but I don't believe it" which cries out for explication. The history of impossible pictures goes back to Pompeii. Impossible pictures should be distinguished from pictures which permit more than one gestalt, such as the duck-rabbit or the candlestick-faces. A research project conducted in the Discipline of Philosophy aims to address the issue on several fronts. Preliminary Classification of Impossible Forms
An Essay by Einstein -- The World As I See It
"How strange is the lot of us mortals! Each of us is here for a brief sojourn; for what purpose he knows not, though he sometimes thinks he senses it. But without deeper reflection one knows from daily life that one exists for other people -- first of all for those upon whose smiles and well-being our own happiness is wholly dependent, and then for the many, unknown to us, to whose destinies we are bound by the ties of sympathy. A hundred times every day I remind myself that my inner and outer life are based on the labors of other men, living and dead, and that I must exert myself in order to give in the same measure as I have received and am still receiving... "I have never looked upon ease and happiness as ends in themselves -- this critical basis I call the ideal of a pigsty. The ideals that have lighted my way, and time after time have given me new courage to face life cheerfully, have been Kindness, Beauty, and Truth. "My political ideal is democracy.
Ludwig Wittgenstein
1. Biographical Sketch Wittgenstein was born on April 26, 1889 in Vienna, Austria, to a wealthy industrial family, well-situated in intellectual and cultural Viennese circles. In 1908 he began his studies in aeronautical engineering at Manchester University where his interest in the philosophy of pure mathematics led him to Frege. Upon Frege's advice, in 1911 he went to Cambridge to study with Bertrand Russell. Russell wrote, upon meeting Wittgenstein: “An unknown German appeared … obstinate and perverse, but I think not stupid” (quoted by Monk 1990: 38f). During his years in Cambridge, from 1911 to 1913, Wittgenstein conducted several conversations on philosophy and the foundations of logic with Russell, with whom he had an emotional and intense relationship, as well as with Moore and Keynes. In the 1930s and 1940s Wittgenstein conducted seminars at Cambridge, developing most of the ideas that he intended to publish in his second book, Philosophical Investigations. 2. 3.
Raptitude.com – Getting Better at Being Human
What is Frege’s ‘concept horse problem’?
DOI:10.1093/acprof:oso/9780199665785.003.0005 Frege’s concept horse problem is often presented as inspiring what the Tractatus has to say about logical category distinctions and the say-show distinction. But what exactly is that problem; how far is it soluble, and how far did Frege suppose it soluble? The chapter argues that the problems commentators have discussed under this rubric in fact constitute a family of distinct sub-problems, some of which Frege regarded as soluble, others of which he regarded as innocuous, and yet others of which he simply ignored. Since the most acute of these sub-problems—the problem of the inexpressibility of logical category distinctions—is one with which Frege did not expressly concern himself in writings available to Wittgenstein, the Tractatus does not—contrary to Peter Geach—derive its distinctive doctrines on these matters from Frege. Oxford Scholarship Online requires a subscription or purchase to access the full text of books within the service.
Cutest Paw Gives You the Cutest Animal Pictures Around the World
The Skeptic Tank -- Extraordinary Claims Require Extraordinary Evidence
stereomood – emotional internet radio - music for my mood and activities