StumbleUpon - Wikipedia, the free encyclop
StumbleUpon is a discovery engine (a form of web search engine) that finds and recommends web content to its users. Its features allow users to discover and rate Web pages, photos and videos that are personalized to their tastes and interests using peer-sourcing and social-networking principles. StumbleUpon acquired 5by in 2013 which its video discovery product.[3] History[edit] StumbleUpon was founded in November 2002[8] by Garrett Camp, Geoff Smith, Justin LaFrance and Eric Boyd during Garrett's time in post-graduate school in Calgary, Canada. The popularity of the software attracted Silicon Valley investor Brad O'Neill to take notice of the company and assist with a move to San Francisco, as well as bringing in subsequent fund-raising totaling $1.2 million from other angel investors including Ram Shriram (Google), Mitch Kapor (Mozilla Foundation), First Round Capital and Ron Conway. Service details[edit] StumbleVideo[edit] StumbleThru[edit] Su.pr[edit] Advertising[edit] Growth[edit]
Mario and Michelle
Answers in Genesis - Creation, Evolution,
Today Noteworthy Video On Demand Answers Conversation After Eden Answers ... with Ken Ham Answers Radio Store New Resources Top Sellers More bestsellers Answers Weekly(news, links & events) Super Specials(discounts & free downloads) cancel Free print newsletter Ken Ham Ken’s blog Previous entries Ken’s Events Answers Worldwide Donate Good News
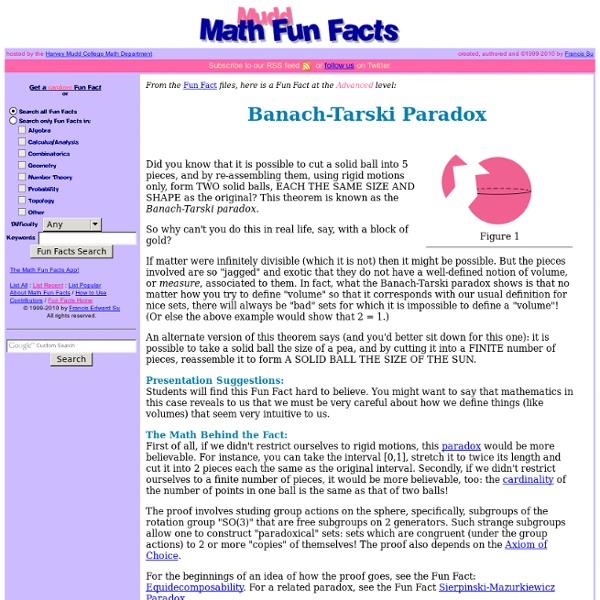
Glass-sphere microscope
A Glass-Sphere Microscope Giorgio Carboni, First draft March 1988 Publication in "Scienza e Vita" December 1993 Publication on this website January 1996 Updated on the 30th of December 2010 Translated by: Sabrina Gemelli, Giacomo Giuli, Karen Coleman Acknowledgments to David W. Walker for his helping in the revision of the English text A snowfall, a flower, a puddle – these all seem like normal things, without surprises. Yet, if you could see the beauty of a snowflake, the hidden shapes of flowers, the variety and the strangeness of the tiny creatures that live in a puddle, you would surely be amazed. You will notice that you are surrounded by a fascinating and unknown world. Usually, while attempting to observe very small objects, we realize the impossibility of distinguishing details smaller than a tenth of millimeter by naked eye. This small instrument will give fairly detailed images if you consider that it is essentially constructed from a small homemade lens. [1] C.L.
Crazy stuff from the bible
. Have I taken things out of context ()? Meanwhile read on... "For I am merciful, saith the Lord, and I will not keep anger forever." "If I testify about myself, my testimony is not valid." "And Jesus coming, spoke to them, saying: All power is given to me in heaven and in earth." And Jesus said, "For judgement I am come into this world." “Love not the world, neither the things that are in the world. "Let your light so shine before men, that they may see your good works, and glorify your Father which is in heaven." "Jacob said, 'I have seen God face to face, and my life is preserved.'" We should fear God (Matthew 10:28) We should love God (Matthew 22:37) There is no fear in love (1 John 4:18) The Arguments from Confusion and Biblical Defects Foolery "But anyone who says 'You fool!' "You fools!" "But God said to him, 'You fool!' "You foolish Galatians!" Feedback: This "foolery" section has been criticised and is discussed further here. Rejoicing Mercy "Blessed are the merciful" [Matthew 5:7]
Wallpaper
Videos See the universe come to life via animations, scientific visualizations, expert commentary, and more.