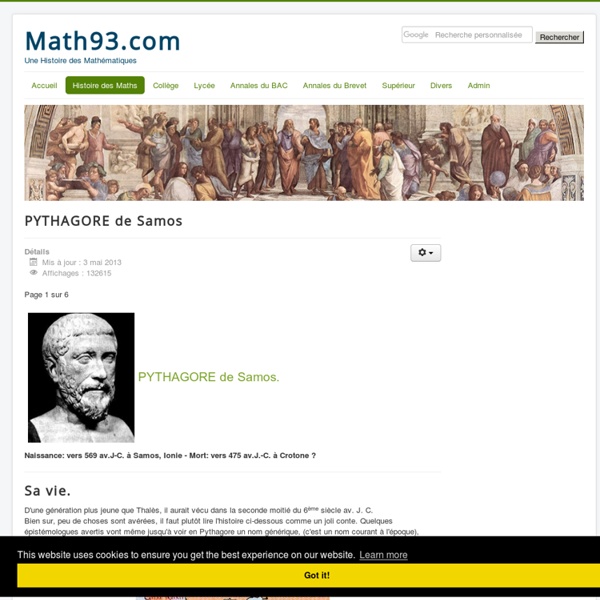
Pythagore Un article de Wikipédia, l'encyclopédie libre. Pythagore (Πυθαγόρας) Philosophe présocratique Antiquité Buste de Pythagore - Musées du Capitole - Rome Pythagore (en grec ancien Πυθαγόρας / Pythagóras) est un réformateur religieux et philosophe présocratique qui serait né aux environs de 580 av. Le néopythagorisme est néanmoins empreint d'une mystique des nombres, déjà présente dans la pensée de Pythagore. D'après un écho marquant d’Héraclide du Pont, Pythagore serait le premier penseur grec à s’être qualifié lui-même de « philosophe[4] ». « Par la même raison, sans doute, tous ceux qui se sont attachés depuis aux sciences contemplatives, ont été tenus pour Sages, et ont été nommés tels, jusques au temps de Pythagore, qui mit le premier en vogue le nom de philosophes. — Cicéron, Tusculanes, V, 3, § 8 Biographie de Pythagore Beaucoup de documents, tardifs, ont été publiés sur la vie de Pythagore[5],[6],[7],[8]. Naissance — Jamblique, Vie de Pythagore, § 7[7]. Adolescence et maturité Instruction
Pythagore «Pythagore est le créateur de la philosophie non seulement parce qu'il saisit le sens de la quête inachevée de l'homme, mais encore parce qu'il offre le terme de cette quête: la réalité éternelle qui explique à la fois le surgissement de l'existence relative et la perfection à laquelle elle est conviée. (...) Quel eût été le destin de la pensée grecque sans Pythagore? C'est de lui que dépendent Parménide, le créateur de l'ontologie, et Platon, le génie qui a donné son orientation définitive à cette pensée; et par le truchement de Platon, Aristote, l'orfèvre qui en a fixé la terminologie.» Yvan Gobry Pythagore a vécu en même temps que Lao-Tsé en Chine, Bouddha en Inde et Zarathoustra en Perse. Pythagore fut d'abord l'homme de la Méditerranée. Fut-il d'abord un maître spirituel, un savant ou un philosophe? Les disciples devaient d'abord faire un noviciat de cinq ans pendant lequel ils s'initiaient au silence. Voici comment Léon Brunschvicg évoque l'apport de Pythagore à l'humanité.
La composition et le nombre d'or 11 mai 2005. construction composition,esquisse,regard,accrochage oeuvre,nombre d’or,composition artistique, Nombre d’or ou Phi Utilisé depuis la nuit des temps [1], dans l’architecture [2] comme dans les œuvres d’arts [3], le nombre d’or est parfois contesté. La construction d’une composition : L’orientation de votre toile/papier est à étudier en premier lieu. Le regard et la composition : Le regard doit-il se porter sur un élément particulier du dessin ou de la peinture ? Construction d’un rectangle d’or Voyez la figure à gauche et en haut pour construire un rectangle d’or : Tracez un carré, du centre d’un des cotés (marqué C) et tracez un arc de cercle passant par un angle opposé. Figure du centre : Reportez la petite longueur sur le petit coté du rectangle. Une esquisse pour vérifier la composition : Imaginez vos sujets sous formes de volumes géométriques simples. L’accrochage de l’œuvre : Créer et contrarier les règles :
Théorème de Pythagore Un article de Wikipédia, l'encyclopédie libre. Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Relation entre les longueurs des côtés dans un triangle rectangle. Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle : le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Ce théorème permet notamment de calculer l’une de ces longueurs à partir des deux autres. Divers autres énoncés généralisent le théorème à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère. Vocabulaire et énoncés Un triangle rectangle est un triangle admettant un angle droit (c’est-à-dire de mesure 90°, ou encore radians). Théorème est rectangle en , alors et
Théorème de Pythagore Cours de quatrième Le théorème de Pythagore est une propriété qui permet de calculer la longueur du troisième côté d'un triangle rectangle lorsqu'on connaît les longueurs des deux autres côtés. Pythagore était un mathématicien de la Grèce antique (en savoir plus). Théorème de Pythagore Vocabulaire Théorème de Pythagore Exemple Utiliser le théorème de Pythagore Pour utiliser le théorème de Pythagore, on doit connaître les longueurs de deux côtés d'un triangle rectangle. Méthode 1. Remarque Le théorème de Pythagore est particulièrement utile pour calculer des longueurs qu'on ne peut pas mesurer, comme des grandes distances sur la Terre ou dans l'espace (astronomie). Réciproque du théorème de Pythagore La réciproque du théorème de Pythagore est une propriété qui permet de dire si un triangle est rectangle ou non lorsqu'on connaît les longueurs de ses 3 côtés. Énoncé Méthode et exemple Bravo pour avoir lu ce cours jusqu'au bout. >>> Le cosinus >>> Le théorème de Pythagore sur cmath.fr Sur le web
Homme de vitruve « [...] que la Nature a distribué les mesures du corps humain comme ceci. Quatre doigts font une paume, et quatre paumes font un pied, six paumes font une coudée : quatre coudées font la hauteur d’un homme. Et quatre coudées font un double pas, et vingt quatre paumes font un homme ; et il a utilisé ces mesures dans ses constructions. Si vous ouvrez les jambes de façon à abaisser votre hauteur d’un quatorzième, et si vous étendez vos bras de façon que le bout de vos doigts soit au niveau du sommet de votre tête, vous devez savoir que le centre de vos membres étendus sera au nombril, et que l’espace entre vos jambes sera un triangle équilatéral. La longueur des bras étendus d’un homme est égale à sa hauteur. Depuis la racine des cheveux jusqu’au bas du menton, il y a un dixième de la hauteur d’un homme. Depuis les tétons jusqu’au sommet de la tête, un quart de la hauteur de l’homme. La main complète est un dixième de l’homme.
Nombre d'or Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b), ce qui s'écrit : avec Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ». (phi), et il est lié à l'angle d'or. Ce nombre irrationnel est l'unique solution positive de l'équation φ2 = φ + 1. L'histoire de cette proportion commence à une période de l'Antiquité qui n'est pas connue avec certitude ; la première mention connue de la division en extrême et moyenne raison apparaît dans les Éléments d'Euclide. Géométrie[modifier | modifier le code] Proportion[modifier | modifier le code] Sa valeur approximative est donc[a] 1,6180339887. , soit un peu moins que , s'écrivant aussi .
Le nombre d'or (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a. a/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = que nous notons Φ et vaut à peu près 1,618... C'est cette valeur qui est appelée le nombre d'or (dit Φ (phi) en hommage au sculpteur grec Phidias qui s'en servit dans les proportions du Parthénon à Athènes. En espagne, deux tableaux de Antonio de Garcia de Pablo, muchas gracias ;): Pour voir les images suivantes en plus grand les cliquer A ce stade, je vous soumets un petit problème que m'a proposé Dominique Payeur : Je dispose d'un capital. Nous pouvons d'ores et déjà noter quelques résultats : On pourrait aussi sans équation du second degré montrer que 1/Φ = Φ - 1. et on a aussi : Les FRACTIONS
Le nombre d'or L' histoire ... Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au XIXème siècle : Adolf Zeising (1810-1876), docteur en philosophie et professeur à Leipzig puis Munich, parle de "section d'or" (der goldene Schnitt) et s'y intéresse non plus à propos de géométrie mais en ce qui concerne l'esthétique et l'architecture.
Vitruve : de l'Architecture : livre 3 1. APOLLON de Delphes déclara, par la bouche de sa pythonisse, que Socrate était le plus sage des mortels. On rapporte que ce philosophe disait, avec autant de raison que de justesse, qu'il eût fallu que les hommes eussent une large ouverture à la poitrine, afin que leurs pensées, loin d'y demeurer cachées, fussent, au contraire, exposées à l'oeil de l'observateur. Et plût aux dieux que, d'accord avec lui, la nature eût donné le moyen de les découvrir, de les apercevoir! 3. 4. 1. 1. 3. 4. 5. 6. 7. 8. 9. II. Chaque sorte de temple se distingue par la forme différente qu'il présente à notre vue. 2. 3. 4. 5. 6. 7. 8. III. 1. 2. 3. 4. 5. 6. 6. 8. 9. 10. 11. 12. 13. IV. 1. 2.
Euclide : éléments de Géométrie (libre VI) 1. Les figures rectilignes semblables sont celles dont les angles sont égaux chacun à chacun et dont les côtés placés autour des angles égaux sont proportionnels. 2. Les figures sont réciproques lorsque les antécédents et les conséquents des raisons se trouvent dans l'une et l'autre figure. 3. 4. 5. Les triangles et les parallélogrammes qui ont la même hauteur sont entre eux comme leurs bases. Soient les triangles ABC, ACD (fig. 121) et les parallélogrammes EC, CF qui ont la même hauteur, savoir, la perpendiculaire menée du point A sur la droite BD : je dis que le triangle ABC est au triangle ACD et que le parallélogramme EC est au parallélogramme CF comme la base BC est à la base CD. Prolongez la droite BD de part et d'autre vers les points H, L, et faites les droites BG, GH égales chacune à la base B C ; faites aussi les droites DK, KL égales chacune à la base CD, et menez les droites AG, AH, AK, AL. Le triangle BDE est égal au triangle CDE (prop. 37. Faites la même construction.
Phi - Le Nombre d'Or - La Divine Porportion - l'ADN Divin Les Romains, les Grecs, les Juifs et les Egyptiens semblaient tous d'accord : 1,618 était le nombre d'or, le nombre de l'harmonie universelle, le nombre de la création, le nombre de Dieu, le Créateur. Lle nombre utilisé partout dans l'ordre caché de la Création et qu'il fallait donc employer dans les édifices dédiés au Créateur afin de s'en rapprocher. Empreint de mystère, objet d'un culte tantôt religieux, tantôt magique, le nombre d'or influence la vision occidentale de l'harmonie. Chez les Grecs, avec le développement de la géométrie, la secte secrète des pythagoriciens en avait fait un symbole d'harmonie universelle, de vie, d'amour et de beauté. Au Moyen-Age, les savants, les pères de l'église, les bâtisseurs, les maîtres d'ouvrages ou maîtres d'oeuvre, se réclament de la doctrine platonicienne des corps cosmiques, les cinq polyèdres réguliers, et ont fait du nombre d'or, "la divine proportion", un modèle de perfection esthétique et philosophique." Le nombre d'Or est appelé Phi
Le nombre d'or dans l'architecture grecque : mythe ou réalité ? Filles des nombres d’or, Fortes des lois du ciel, Sur nous tombe et s’endort, Un Dieu couleur de miel. Paul Valéry, « Cantique des Colonnes ». Le nombre d’or est un nombre égal à (1+√5)/2, soit environ 1,618 et correspond à une proportion considérée comme particulièrement esthétique. Il apparaît dans la pensée grecque avec Pythagore, au tournant du VIème et du Vème siècle avant J. Cette proportion, pour de nombreux artistes comme Léonard de Vinci ou encore Le Corbusier -pour ne citer que les plus célèbres-, donnerait la clef de l’harmonie d’une œuvre d’art. Mais dans quelle mesure n’y a-t-il pas là un mythe architectural ? Quelques propriétés mathématiques La section d’or La définition géométrique de la section dorée par Euclide est celle qui coupe un segment a + b en établissant une relation telle que : (a + b)/a = a/b. La célèbre suite de Fibonacci, mathématicien du XIIIème siècle, entretient des liens étroits avec φ. Pentagramme étoilé Triangle de module Phi φ dans l’architecture grecque