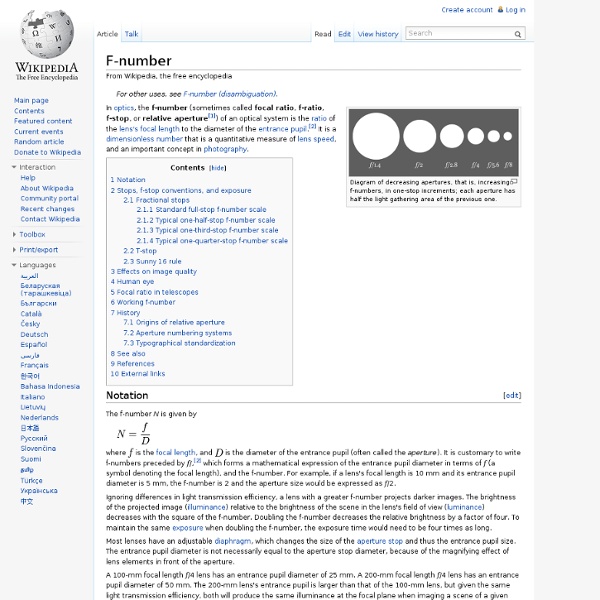
F-number

Diagram of decreasing apertures, that is, increasing f-numbers, in one-stop increments; each aperture has half the light gathering area of the previous one. In optics, the f-number (sometimes called focal ratio, f-ratio, f-stop, or relative aperture[1]) of an optical system is the ratio of the lens's focal length to the diameter of the entrance pupil.[2] It is a dimensionless number that is a quantitative measure of lens speed, and an important concept in photography. Notation[edit] The f-number N is given by where is the focal length, and is the diameter of the entrance pupil (effective aperture). A 100 mm focal length f/4 lens has an entrance pupil diameter of 25 mm. A T-stop is an f-number adjusted to account for light transmission efficiency. Stops, f-stop conventions, and exposure[edit] A Canon 7 mounted with a 50 mm lens capable of an exceptional f/0.95 A 35 mm lens set to f/11, as indicated by the white dot above the f-stop scale on the aperture ring. f/1 = , f/1.4 = , f/2 = , f/2.8 = (i.e.,

Het verschil tussen full-frame en crop sensor - Maarten van de Kamp Full-frame sensoren worden gebruikt in het duurste en meest professionele segment van fotografie, waar crop sensoren, zoals de APS-C sensor, ingebouwd worden in de instap en semi-professionele segmenten van fotografie. Dit artikel gaat specifiek over de verschillen tussen de full frame sensor en een sensor met een cropfactor. Over de bijbehorende objectieven kun je lezen in dit artikel. Full-frame sensor Een full-frame sensor is een sensor met de afmetingen van 36 x 24 mm (breedte x hoogte). De reden dat dit full-frame heet is om dat dit formaat overeenkomt met de afmetingen van fotorolletjes. Voordelen t.o.v. crop sensor Een full-frame sensor heeft als voordeel dat er meer ruimte is tussen de gevoelige pixels waardoor er minder kans is op ruisvorming. Een voorbeeld van deze scherptediepte: Een Canon EOS 5D Mk II met een 70 – 200 f/2.8 lens kan over het gehele bereik een diafragma van f/2.8 gebruiken. Crop sensor Voordelen t.o.v. full-frame Het concrete verschil Het verschil met voorbeelden:

Composities met kleur | DIGITALE•FOTOGRAFIETIPS Kleur is een enorm belangrijk compositie element in je foto’s. Kleur kan een emotionele reactie van de kijker uitlokken en voegt een visuele impact toe aan de foto. Kleuren zijn diepgeworteld in de visuele cultuur. Met kleur grijp je de aandacht van de kijker, felle kleuren doen het altijd goed. Canon EOS 5DmkII, 73mm, 1/125s op f/4, ISO 1600 Maar een andere belangrijke functie van kleur in je compositie is om een sfeergevoel mee te geven door middel van het kleurgebruik en dan kan kleur juist heel subtiel worden ingezet. Door aandacht te besteden aan deze twee functies van kleur in je composities stijgt je foto boven de middenmoot uit. Eigenschappen van kleur Kleur heeft een aantal eigenschappen die van belang zijn voor het beoordelen van de toepassing. Hue geeft de kleuren van het kleurenspectrum aan. De kleurverzadiging geeft aan hoeveel kleur er aanwezig is. Licht geeft aan waar de tint of toon van een kleur zit tussen de twee uitersten van zwart en wit. Licht Kleurverzadiging Blauw Groen