


VISUALISER LA COURBURE Comprendre la notion de courbure sans aucune formule... Du simple rayon de courbure jusqu’au tenseur de Riemann, clé de voûte de la géométrie différentielle. Panorama non exhaustif ! « La géométrie est la science des raisonnements corrects sur des figures incorrectes », George Pólya, How to solve it, Princeton 1957. [1] Certaines notions géométriques semblent très intuitives. Habitués que nous sommes à notre expérience sensorielle, les représentations visuelles nous guident parfois habilement dans la compréhension de concepts géométriques. L’exemple que nous allons développer ici est celui de la courbure. Le mathématicien étudie souvent des objets ou des espaces si complexes que toute représentation visuelle serait une tentative futile, vouée à l’échec. En effet, un cylindre est pour le mathématicien un objet plat ! Pour s’en convaincre, il ne faut pas voir le cylindre comme un objet qui roule si on le pose sur une table. Une représentation fidèle de cet espace est la suivante :
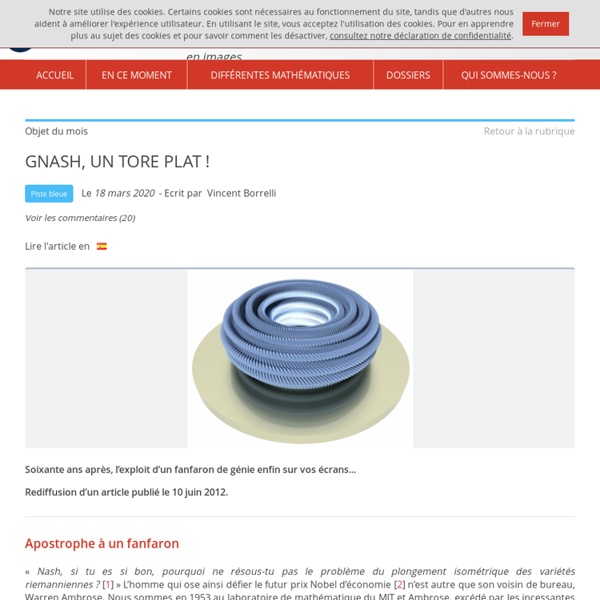
Un tore carré et plat | Pour la Science En 1961, Pearl Buck écrivit : « Toute chose est possible tant qu'elle ne s'est pas révélée impossible – et même en ce cas, elle ne l'est peut-être que provisoirement. » Elle aurait pu citer John Nash en exemple. Dans les années 1950, ce mathématicien américain (prix Nobel d'économie en 1994, prix Abel en 2015 et mort dans un accident de voiture en mai 2015) découvrit à la surprise générale qu'un problème géométrique réputé impossible avait en réalité des solutions en abondance. Quelques pages d'arguments mathématiques lui suffirent pour passer de l'impossible au possible, en détruisant au passage un certain nombre de certitudes et d'intuitions. Le problème en question est celui du « plongement isométrique » : en deux mots – nous y reviendrons –, il s'agit d'une transformation qui fait passer d'un plan à une surface courbe en conservant toutes les distances. Mais il y avait un détail. Surfaces et portions de plan On oublie la forme
SURFER | IMAGINARY Mathématiquement, le programme illustre la géométrie algébrique réelle en temps réel. Les surfaces exhibées sont obtenues comme l’ensemble des zéros d’une équation polynomiale en les variables x, y et z. Tous les points de l’espace qui résolvent l’équation sont représentés et forment la surface. Regardez par exemple x2+y2+z2-1=0, l’équation de la sphère. Vous pouvez facilement voir que le point (x,y,z)=(0,0,0) n’est pas sur la sphère, alors que les points (1,0,0), (0,1,0) et (0,0,-1) sont solutions de l’équation. Le programme inclut une grande galerie d’exemples avec des explications et un tutoriel. Le grand avantage de SURFER est qu’il n’est pas besoin de comprendre a priori les mathématiques sous-jacentes (la géométrie algébrique), vous pouvez expérimenter, essayer, suivre votre intuition et votre créativité et de cette manière apprendre des maths et créer vos oeuvres d’art personnalisées telles que des images ou des animations.
Cours de maîtrise de math, M.M.D. B.2.: Courbes, surfaces et sous-variétés On trouvera ici, mise en ligne suivant l'avancement du cours, mes notes personnelles - incomplètes, les énoncés des devoir, ainsi que quelques sujets d'examen des années précédentes. Syllabus, au format ps ou pdf. Texte complet, chapitres 1 à 6, au format ps ou pdf. Notes sur le chapitre 1, au format ps ou pdf. Court rappel de calcul différentiel, au format ps ou pdf. Examen final de Janvier 2004, au format ps ou pdf. Archives 2002-03: Enoncé du devoir no 1, au format ps ou pdf. Back to my web page.
Géométrie non euclidienne In about 300 BC Euclid wrote The Elements, a book which was to become one of the most famous books ever written. Euclid stated five postulates on which he based all his theorems: To draw a straight line from any point to any other. To produce a finite straight line continuously in a straight line. Proclus (410-485) wrote a commentary on The Elements where he comments on attempted proofs to deduce the fifth postulate from the other four, in particular he notes that Ptolemy had produced a false 'proof'. Playfair's Axiom:- Given a line and a point not on the line, it is possible to draw exactly one line through the given point parallel to the line. Although known from the time of Proclus, this became known as Playfair's Axiom after John Playfair wrote a famous commentary on Euclid in 1795 in which he proposed replacing Euclid's fifth postulate by this axiom. To each triangle, there exists a similar triangle of arbitrary magnitude. Here is the Saccheri quadrilateral .
Retournement du tore De quoi parle-t-on ? La topologie étudie les figures à déformations près. Par exemple, vous pouvez déformer une tasse en un tore plein ; un « mug » en un « doughnut » chez les anglo-saxons. Recollements et déchirements interdits Dans le sujet dont je veux vous entretenir, il s’agit de déformer des surfaces dans l’espace, mais pour illustrer certaines notions, je vais comme ci-dessus utiliser des déformations de courbes dans le plan. Quelles sont les figures autorisées ? Immersion : auto-intersections autorisées. Courbe lise, courbes non lises Dans le problème considéré ici, on va regarder des déformations continues (on ne saute pas directement d’un état à l’autre). Pour une immersion, non seulement les déchirures sont interdites, mais les plis également. (Animation se déroulant dans un plan). Tentative avortée d’éversion de la sphère : vue externe et vue en coupe. Revenons aux surfaces. Attention, c’est difficile ! Il se trouve que pour le tore, un retournement est plus facile à trouver.
Bouteille de Klein Construction[modifier | modifier le code] Voici un plan de montage dans ℝ3. À partir du carré initial, on colle les deux bords rouges l'un contre l'autre, dans le sens des flèches. Si les deux segments bleus étaient orientés de la même façon, le recollement des segments opposés donnerait un tore. Autre méthode de construction[modifier | modifier le code] La bouteille de Klein peut aussi être obtenue par recollement de deux rubans de Möbius le long de leurs bords. On se donne deux exemplaires d'un tel carré, et on obtient deux exemplaires de ruban de Möbius en faisant cette fois d'abord l'identification suivant les flèches bleues. Il est peut-être plus facile de voir qu'une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius. Paramétrisation[modifier | modifier le code] est un paramètre qui suit le corps de la bouteille tandis que évolue le long de sa section. [Information douteuse][réf. nécessaire] est le rayon de ce cercle. Portail de la géométrie
Transformation de Möbius En mathématiques, et plus particulièrement en géométrie, les transformations de Möbius sont de manière générale des automorphismes du compactifié d'Alexandrov de noté , définies comme la composée d'un nombre fini d'inversions par rapport à des hyperplans ou des hypersphères. En particulier, si on identifie à la sphère de Riemann , alors on peut prouver que les transformations de Möbius conservant l'orientation sont de la forme : avec a, b, c et d quatre complexes tels que ad – bc ≠ 0, la formule ci-dessus étant à prendre au sens suivant si z = ∞ ou si cz + d = 0 : Définition générale[modifier | modifier le code] Soit n un entier naturel, on munit ℝn de sa structure euclidienne canonique et on définit alors les inversions de par rapport à un hyperplan ou à une hypersphère (qu'on appellera parfois plan et sphère par abus de langage) : De plus, ces inversions sont des homéomorphismes. Définition — L'ensemble des transformations de Möbius, est le sous-groupe des homéomorphismes de . , on note . sur . de
Nombre d'Euler Christian RONSE © (02/11/2007) LSIIT UMR 7005 CNRS-ULP, Département d'Informatique de l'ULP Le Nombre d'Euler est un entier associé à toute surface orientable. C'est un invariant topologique de celle-ci, dans le sens qu'il ne change pas si la surface subit une déformation continue. Ce nombre ne dépend pas du choix du graphe planaire. S = 15, A = 21, F = 7, donc E = 15 - 21 + 7 = 1. Si cette figure est bornée, toutes les composantes connexes du fond sont des trous de la figure, à l'exception de celle entourant toute la figure ; donc le nombre d'Euler sera égal au nombre de composantes connexes de la figure, moins le nombre de composantes connexes du fond, plus un. Pour les figures dans le plan discret Z2, la définition du nombre d'Euler est celle basée sur le nombre de composantes connexes de la figure et du fond. Ek = Ck(F) - Ck'(B) + 1, où Ck(F) est le nombre de composantes k-connexes de F, et Ck'(B) est nombre de composantes k'-connexes de B. On peut expliquer ces formules.