

Matematicas Visuales | Plane developments of geometric bodies (1): Nets of prisms A right prism is a polyhedron that has two congruents pararel polygonal faces (bases of the prism) and with all remaining faces are rectangles. The main interest of this page is to see how a right prism can be developed into a plane net. There is a platonic solid that is a prism, the cube. This is a cube net: The lateral surface area of a prism is the sum of the areas of the rectangles that form the faces that are not bases of the prism. In the examples above bases were regular polygons. A non-regular hexagonal prism: And its plane net: Another example, plane net of a non-regular triangular prism: The formula for calculating the lateral surface area is the same as before.
Jeux de calcul en flash Jeux de calcul en Flash a. Des Additions avec Scooby b. Jeux Numériques Jeux Numériques > TracenPoche Instrumenpoche Instrumenpoche est une interface qui permet à la fois de créer et visualiser des constructions géométriques animées. Instrumenpoche propose tous les instruments de géométrie usuels : crayon, compas, règle, équerre, rapporteur… ainsi que la possibilité de placer des points nommés, créer des textes mathématiques, un repère, des courbes de fonctions, des codages de longueur ou d’angle droit. Toute construction géométrique créée avec Instrumenpoche peut être visualisée pas à pas, comme un film. La bibliothèque du site Instrumenpoche.net contient de nombreuses constructions de base ou plus sophistiquées. Le site des manuels Sésamath propose la correction de nombreux exercices réalisées avec Instrumenpoche. Pour une utilisation plus avancée, Instrumenpoche est entièrement paramétrable. Interface Instruments Aide pour le maniement des instruments virtuels de géométrie : Autres outils Voir aussi : Utilisateurs avancés Tutoriels Le langage de script Les objets du script : Autres pages de référence :
Calcul volume Facile d’usage, un outil formidable qui vous permet de calculer en mètres cubes tous les volumes dont vous pourrez avoir besoin, mais aussi pour aider vos enfants et vérifier leurs résultats sans prendre le risque de vous tromper. Une exactitude parfaite grâce aux formules qu’elle contient, pratique pour déterminer la masse des différents solides, cubes, cylindres, sphères, etc. Nous vous conseillons également ( Calculatrices & Outils )... Calculatrice credit Le meilleur moyen de connaître les mensualités que vous allez mettre en place et leur durée, en fonction de la somme que vous empruntez et aussi du taux d’intérêts qui vous a été accordé par la banque ! Calcul votre crédit Calculer votre IMC Le calcul qui tient compte de votre taille et de votre poids, vous donnant ainsi un indice en rapport avec votre masse corporelle qui est alors décrétée fluette, parfaite ou sujette à l’embonpoint ! Calcul de votre IMC Perdre du poids Calcul perte de poids
Waterman Polyhedra Play with the controls! Use the "Sequence" slider to step through the series of polyhedra. Click the "Colors" button. If you have red-blue 3D glasses, change the "Stereo Mode" to "Anaglyph". If you have a ColorCode ViewerTM (see below), change the "Stereo Mode" to "ColorCode". Further instructions are below the applet. More Java applets here. Contents: Browser/Java Notes: This is a Java 1.1 applet. Getting Started: Click either one of the Detach buttons (they are identical in function). Advice on using the slider controls: For tiny adjustments, click the end buttons (the arrows). Free 3D glasses are available from Rainbow Symphony. The "Sequence" Slider This slider allows you to explore the first 3000 polyhedra of the infinite series (there is a different series for each origin choice). Since there are 3000 different settings, the slider is very sensitive: Dragging the slider produces a large change. Larger Sequence settings produce complex polyhedra that are nearly spherical. Historical Notes:
Interactive Mathematics Miscellany and Puzzles Math Topics for Exercise PROBLEMES CYCLE III S'inscrire Attention mot de passe Problèmes : sommaire Mesure d'audience ROI statistique webanalytics par <img width="39" height="25" src="
Apprendre les tables de multiplication et d'addition sur internet Opérations Note : On utilise pour réaliser ces divisions les tableaux et étiquettes proposés ici. Diviser par un multiple de 10 On prend en compte le même nombre de chiffres au dividende qu’au diviseur. On les relie avec un arc de cercle pour indiquer que dans un premier temps, il n’y a que ces chiffres qui nous intéressent. On cache le chiffre des unités de chaque côté pour chercher combien il y a de fois 9 dans 6, et on revient ainsi à une situation simple de division à un chiffre au diviseur. Même chose ici et on cherche combien il y a de fois 9 dans 68, la réponse est 7 : 7X9=63. On calcule le produit 7X90 = 630, que l’on soustrait à 683. Diviser par un nombre à deux chiffres ne se terminant pas par o Ici les choses se compliquent, mais on va utiliser la même méthode que décrite précédemment : La technique est la même que ci-dessus (on cache le chiffre des unités de chaque côté), mais il va falloir ici faire des essais. On descend le 6 comme la flèche l’indique.
Multiples and Factors In this activity, students identify multiples and factors and solve problems that involve finding highest common factors and lowest common multiples. Students will need a good recall of multiplication basic facts in order to be able to do these activities. Activity One and Game Discuss the definitions of multiples and factors (on the student book page) before your students begin this activity. Make sure that they understand that every number is a factor of itself, because if they divide a number by itself, there is no remainder. This game could be extended by asking: • What are all the different products you could throw with the two game dice, one labelled 1–6 and the other 4–9? • There are two different ways of getting a product of 12: throwing a 3 and a 4 or a 2 and a 6. • What’s the probability of throwing a double? • Which squares in the game are easier/harder to cover? Harder to cover: a prime number [only 2 out of 36 combinations] and a multiple of 7 [only 6 chances out of 36].)
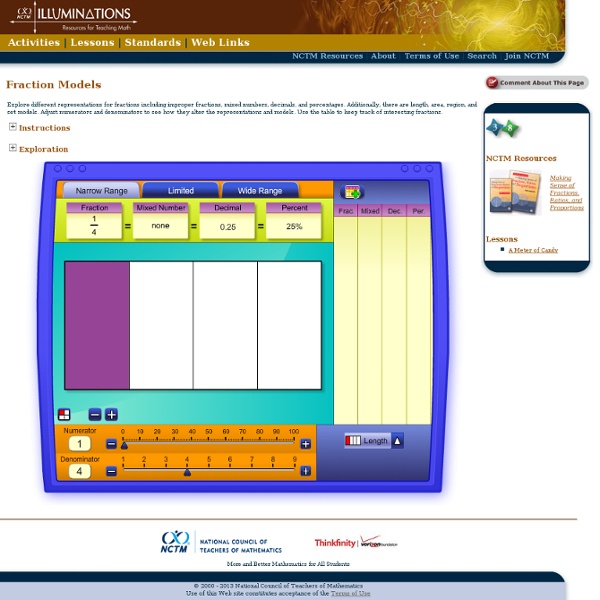
Adding Fractions with the Same Denominator | Help With Fractions Adding fractions with the same denominators is pretty straightforward when you follow the rules. This lesson covers adding fractions with same denominator. We will include all of the information you will need to make working with common denominator problems a breeze! The equation above shows the Rule for addition. To add fractions, the denominators must be equal. Build each fraction (if needed) so that both denominators are equal.Add the numerators of the fractions.The new denominator will be the denominator of the built-up fractions.Reduce or simplify your answer, if needed. That’s all there is to it! Here’s an example of adding fractions with the same denominator… Do you want to take a moment to check your work? Now that you have this part of adding fractions down, let’s dig a little deeper… You do want to be a “whiz” at fractions? Okay then! It would be great if the rule as stated above was all you needed to know about adding fractions. How to Simplify Your Answers Here’s the situation.