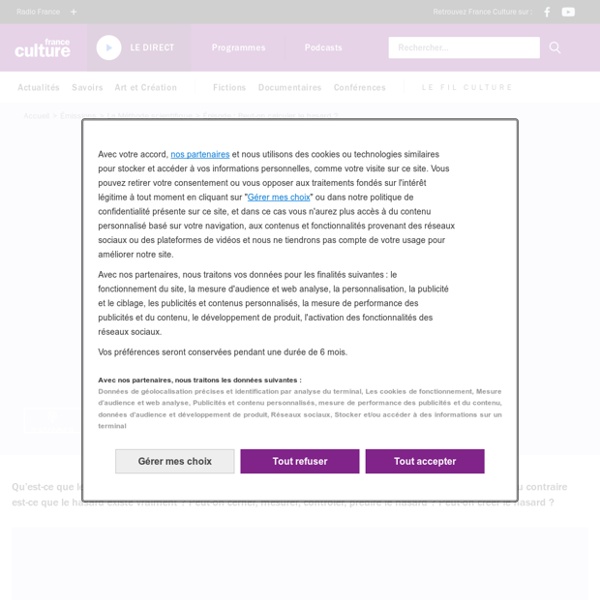
La machine Enigma: son fonctionnement
L'entre-deux-guerres voit le début de la mécanisation de la cryptographie. Des outils mécaniques, comme les cylindres chiffrants, sont mis à disposition des opérateurs, et des machines électromécaniques, sont mises au point. Ces machines fonctionnent sur le principe des rotors et des contacts électriques, afin de réaliser des formes de substitution polyalphabétique dont la clef a une longueur gigantesque de l'ordre de centaines de millions de lettres, au lieu de quelques dizaines dans les méthodes artisanales, comme le chiffre de Vigenère. Enigma est la machine à chiffrer et déchiffrer qu'utilisèrent les armées allemandes du début des années trente jusqu'à la fin de Seconde Guerre Mondiale. Le côté génial de cette machine est que même si elle tombe entre les mains ennemies, sa sécurité n'est pas compromise. Position des rotors : 2 - 3 - 1 Orientations des rotors : 2 - 23 - 5 Branchements des connexions : A/L - P/R - T/D - B/W - K/F - O/Y Indicateurs : B - W - E Au final, on a:
Biographie de Alan Turing
Turing est une des grandes figures du XXè siècle dont la mémoire n'a été que récemment réhabilitée. Il est pourtant le père des ordinateurs modernes, au moins pour leur partie théorique. Sa contribution à la victoire des alliés pendant la Seconde Guerre mondiale est décisive. Mais un suicide prématuré, peut-être "encouragé" par les autorités britanniques, son homosexualité, l'ont plongé un temps dans l'anonymat de l'histoire. Alan Mathison Turing est né le 23 juin 1912 à Londres. C'est ainsi qu'il réussit en 1931 l'examen d'entrée au très sélectif King's College de Cambridge. En 1936, Turing part faire son doctorat à Princeton (Etats-Unis). Après la guerre, Turing travaille à l'institut de Physique de Grande-Bretagne à la conception des premiers ordinateurs. À titre posthume, la reine Elizabeth a accordé à Turing la grâce royale pour sa condamnation le 24 décembre 2013… près de 60 ans après sa mort ! Les entrées du Dicomaths correspondant à Turing
L'aire du disque d'Archimède, démonstration et animation en flash
Archimède π, euréka ! (1) WANTED π CLIQUER les images des animations puis OUVRIR puis DOUBLE CLIQUER r l'animation en swf ou en .exe Euclide, Archimède, Appolonius, Viète et bien d'autres se sont attaqués au calcul du développement décimal du nombre π . Archimède et l'aire du disque Les travaux d'Archimède sur le calcul des aires et des volumes constituent l'apogée de la géométrie alexandrine. Le disque est découpé en de nombreux triangles isocèles (12 ici). Autre animation Où le disque se transforme en parallélogramme. Cliquer Archimède... π , euréka... Achimède ( environ 287-212 avant notre ère) est considéré avec Euclide comme le plus grand mathématicien de l'Antiquité. Le calcul de la longueur du côté du polygone régulier revient à dresser une table des sinus et nécessite un algorithme de calcul de racines carrées. Archimède avait observé que toute sphère vaut 4 cônes ayant pour base son grand cercle et pour hauteur son rayon. Une décomposition de la sphère... avec des petites pyramides
Les nombres premiers
Si on y arrive, n est le produit de 2 nombres. Ci-dessus : 12 = 3 (lignes) x 4 (colonnes). On dit que n est un nombre composé. Si on n’y arrive pas, n ne se décompose pas en produit de deux nombres, on dit que n est un nombre premier. On voit ci-dessous que 7 est un nombre premier. Un nombre premier est donc un nombre dont ses seuls diviseurs sont 1 et lui-même. Amusez-vous à leurs trouver un diviseur autre que 1 ou eux-mêmes …! Les plus anciennes traces des nombres premiers ont été trouvées près du lac Edouard au Zaïre sur un os (de plus de 20000 ans), l’os d’Ishango, recouvert d’entailles marquant les nombres premiers 11, 13, 17 et 19. On peut supposer aussi, que par leurs travaux sur les nombres, égyptiens et babyloniens ont certainement été menés à rencontrer des nombres premiers, mais nous ne possédons aucune preuve à ce sujet. Par exemple, 28 est un nombre parfait, car 28 = 1 + 2 + 4 + 7 + 14. C’est avec Euclide d'Alexandrie (-320? Image M.Qrius
Centre Presse : Lavoux - Poitiers: Jean-Yves a choisi la voiture électrique
Pour ses trajets domicile-travail, Jean-Yves Osset a choisi la voiture électrique. Un peu moins chère et surtout plus écolo. Il ne changerait plus. Depuis un an, Jean-Yves Osset quitte chaque matin son pavillon de Lavoux au volant de sa voiture électrique, direction le centre-ville de Poitiers et sa médiathèque où il travaille. « J'ai longtemps hésité avant de me lancer mais franchement, sur le marché des occasions récentes, on trouve désormais des voitures électriques à prix abordable. Pour 7.000 euros, on a un véhicule dans les 30.000 km au compteur. » Sa Zoé, il l'a achetée 10.000 euros à l'époque. « Au final, c'est juste un peu moins cher » Jean-Yves s'y retrouve aussi financièrement, « même si ce n'est pas du simple au double. en savoir plus Comment participer à cette série ? Nous vous invitons à participer à notre série sur la mobilité en ruralité et à nous faire connaître vos initiatives ou celles observées dans votre commune.
fraction irréductible décomposition en produit de facteurs premiers
Exercice 1: Décomposition en produit de facteurs premiers - Transmath Cinquième Quatrième Troisième Décomposez et en produit de facteurs premiers. En utilisant ces décompositions, simplifiez au maximum la fraction . Exercice 2: Simplifier une fraction à l'aide de la décomposition en facteurs premiers - Nombre premier - Transmath Cinquième Quatrième Troisième Simplifier à l'aide de la décomposition en produit de facteurs premiers. Exercice 3: Simplifier une fraction - décomposition en produit de facteurs premiers - Transmath Quatrième Troisième Décomposer en produit de facteurs premiers : Dans chaque cas, simplifier la fraction, puis vérifier avec la calculatrice: Exercice 4: décomposition en produit de facteurs premiers - Transmath Quatrième Troisième À l’aide de la calculatrice, décomposer et en produits de facteurs premiers. Exercice 5: Rendre une fraction irréductible à l'aide d'une décomposition en produit de facteurs premiers - Transmath Quatrième Troisième
Leonardo Fibonacci, découvreur du nombre d’or | France Inter
Fils d’un marchand et notaire public des douanes, Leonardo Fibonacci (1175 - 1250) fait son éducation au Maghreb. Les traités de paix en cours de signature entre les cités italiennes et les pouvoir musulmans locaux permettent à celles-ci d'ouvrir des comptoirs commerciaux. Le père de Leonardo doit calculer les taxes de ces marchandises, et ces calculs sont parfois fastidieux, d'autant plus qu'ils sont écrits en chiffres romains. Faits de lettres, comme le V pour 5 ou le X pour 10, les calculs sont difficiles, alors les marchands utilisent des abaques, mais ceux-ci ont aussi leurs limites. La découverte du zéro Léonardo découvre les lieux, se fait des amis, apprend les chiffres arabes et découvre alors un objet mathématique inconnu des occidentaux : le zéro. Retour en Italie, les mathématiques et le nombre d'or De retour à Pise, il sera ainsi le passeur du chiffre zéro en Europe, certain que ce zéro et les chiffres arabes vont résoudre les problèmes de calculs quotidiens des marchands.