Complex or imaginary numbers - A complete course in algebra The defining property of i The square root of a negative number Powers of i Algebra with complex numbers The real and imaginary components Complex conjugates IN ALGEBRA, we want to be able to say that every polynomial equation has a solution; specifically, this one: x2 + 1 = 0. That implies, x2 = −1. But there is no real number whose square is negative. i2 = −1. That is the defining property of the complex unit i. In other words, i = The complex number i is purely algebraic. Example 1. 3i· 4i = 12i2 = 12(−1) = −12. Example 2. −5i· 6i = −30i2 = 30. We see, then, that the factor i2 changes the sign of a product. Problem 1. To see the answer, pass your mouse over the colored area. The square root of a negative number If a radicand is negative -- , where a > 0, -- then we can simplify it as follows: = i In other words: The square root of −a is equal to i times the square root of a. Problem 2. Powers of i Let us begin with i0, which is 1. And we are back at 1 -- the cycle of powers will repeat. 1, i, −1, or −i
Vieta's formulas In mathematics, Vieta's formulas are formulas that relate the coefficients of a polynomial to sums and products of its roots. Named after François Viète (more commonly referred to by the Latinised form of his name, Franciscus Vieta), the formulas are used specifically in algebra. The Laws[edit] Basic formulas[edit] Any general polynomial of degree n (with the coefficients being real or complex numbers and an ≠ 0) is known by the fundamental theorem of algebra to have n (not necessarily distinct) complex roots x1, x2, ..., xn. Equivalently stated, the (n − k)th coefficient an−k is related to a signed sum of all possible subproducts of roots, taken k-at-a-time: for k = 1, 2, ..., n (where we wrote the indices ik in increasing order to ensure each subproduct of roots is used exactly once). The left hand sides of Vieta's formulas are the elementary symmetric functions of the roots. Generalization to rings[edit] belong to the ring of fractions of R (or in R itself if 's are computed from the 's. and
Complex plane Geometric representation of z and its conjugate z̅ in the complex plane. The distance along the light blue line from the origin to the point z is the modulus or absolute value of z. The angle φ is the argument of z. In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis. It can be thought of as a modified Cartesian plane, with the real part of a complex number represented by a displacement along the x-axis, and the imaginary part by a displacement along the y-axis.[1] Notational conventions[edit] In complex analysis the complex numbers are customarily represented by the symbol z, which can be separated into its real (x) and imaginary (y) parts, like this: for example: z = 4 + 5i, where x and y are real numbers, and i is the imaginary unit. In the Cartesian plane the point (x, y) can also be represented in polar coordinates as where Stereographic projections[edit] Cutting the plane[edit]
Complex Numbers A Complex Number A Complex Number is a combination of a Real Number and an Imaginary Number Real Numbers are numbers like: Nearly any number you can think of is a Real Number! Imaginary Numbers when squared give a negative result. Normally this doesn't happen, because: when we square a positive number we get a positive result, and when we square a negative number we also get a positive result (because a negative times a negative gives a positive), for example −2 × −2 = +4 But just imagine such numbers exist, because we will need them. The "unit" imaginary number (like 1 for Real Numbers) is i, which is the square root of −1 Because when we square i we get −1 i2 = −1 Examples of Imaginary Numbers: And we keep that little "i" there to remind us we need to multiply by √−1 Complex Numbers A Complex Number is a combination of a Real Number and an Imaginary Number: Examples: Can a Number be a Combination of Two Numbers? Can we make up a number from two other numbers? We do it with fractions all the time.
Matrix (mathematics) Each element of a matrix is often denoted by a variable with two subscripts. For instance, a2,1 represents the element at the second row and first column of a matrix A. Applications of matrices are found in most scientific fields. In every branch of physics, including classical mechanics, optics, electromagnetism, quantum mechanics, and quantum electrodynamics, they are used to study physical phenomena, such as the motion of rigid bodies. The numbers, symbols or expressions in the matrix are called its entries or its elements. The size of a matrix is defined by the number of rows and columns that it contains. Matrices are commonly written in box brackets: An alternative notation uses large parentheses instead of box brackets: The entry in the i-th row and j-th column of a matrix A is sometimes referred to as the i,j, (i,j), or (i,j)th entry of the matrix, and most commonly denoted as ai,j, or aij. Sometimes, the entries of a matrix can be defined by a formula such as ai,j = f(i, j).
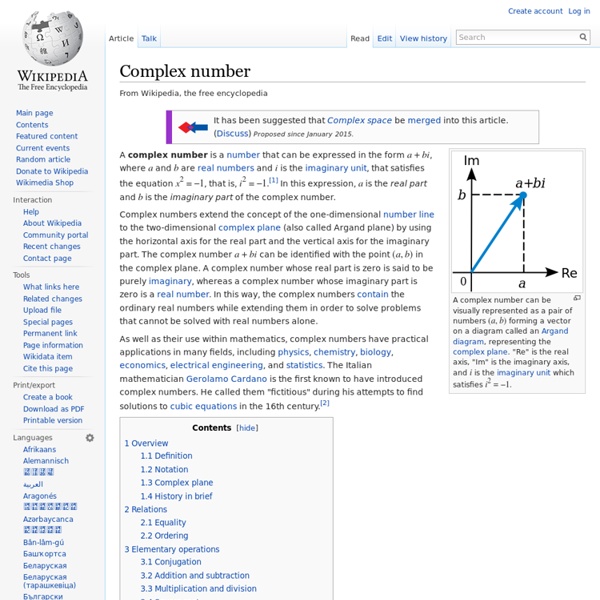
Imaginary unit i in the complex or cartesian plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis There are in fact two complex square roots of −1, namely i and −i, just as there are two complex square roots of every other real number, except zero, which has one double square root. In contexts where i is ambiguous or problematic, j or the Greek ι (see alternative notations) is sometimes used. For the history of the imaginary unit, see Complex number: History. Definition[edit] With i defined this way, it follows directly from algebra that i and −i are both square roots of −1. Although the construction is called "imaginary", and although the concept of an imaginary number may be intuitively more difficult to grasp than that of a real number, the construction is perfectly valid from a mathematical standpoint. Similarly, as with any non-zero real number: i and −i[edit] and are solutions to the matrix equation Proper use[edit] (incorrect). (ambiguous). Similarly: Powers[edit]
Complex Number -- from Wolfram MathWorld The complex numbers are the field of numbers of the form , where and are real numbers and i is the imaginary unit equal to the square root of . is used to denote a complex number, it is sometimes called an "affix." can be written . The set of complex numbers is implemented in the Wolfram Language as Complexes. can then be tested to see if it is complex using the command Element[x, Complexes], and expressions that are complex numbers have the Head of Complex. Complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. Through the Euler formula, a complex number may be written in "phasor" form Here, is known as the complex modulus (or sometimes the complex norm) and is known as the complex argument or phase. , where the dashed circle represents the complex modulus of and the angle represents its complex argument. Unlike real numbers, complex numbers do not have a natural ordering, so there is no analog of complex-valued inequalities.
Mathematical induction Mathematical induction can be informally illustrated by reference to the sequential effect of falling dominoes. Mathematical induction is a method of mathematical proof typically used to establish a given statement for all natural numbers. It is done in two steps. The first step, known as the base case, is to prove the given statement for the first natural number. The second step, known as the inductive step, is to prove that the given statement for any one natural number implies the given statement for the next natural number. Although its namesake may suggest otherwise, mathematical induction should not be misconstrued as a form of inductive reasoning (also see Problem of induction). History[edit] An implicit proof by mathematical induction for arithmetic sequences was introduced in the al-Fakhri written by al-Karaji around 1000 AD, who used it to prove the binomial theorem and properties of Pascal's triangle. Description[edit] Example[edit] Algebraically: Axiom of induction[edit]
Euler's formula This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic. Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x, Euler's formula is ubiquitous in mathematics, physics, and engineering. History[edit] It was Johann Bernoulli who noted that[3] And since the above equation tells us something about complex logarithms. Bernoulli's correspondence with Euler (who also knew the above equation) shows that Bernoulli did not fully understand complex logarithms. Meanwhile, Roger Cotes, in 1714, discovered that ("ln" is the natural logarithm with base e).[4] Applications in complex number theory[edit] where the real part the imaginary part atan2(y, x) . and that both valid for any complex numbers a and b. . . and
Complex Numbers: Introduction Complex Numbers: Introduction (page 1 of 3) Sections: Introduction, Operations with complexes, The Quadratic Formula Up until now, you've been told that you can't take the square root of a negative number. That's because you had no numbers which were negative after you'd squared them (so you couldn't "go backwards" by taking the square root). Every number was positive after you squared it. So you couldn't very well square-root a negative and expect to come up with anything sensible. Now, however, you can take the square root of a negative number, but it involves using a new number to do it. (But then, when you think about it, aren't all numbers inventions? Anyway, this new number was called "i", standing for "imaginary", because "everybody knew" that i wasn't "real". Then: Now, you may think you can do this: But this doesn't make any sense! Simplify sqrt(–9). (Warning: The step that goes through the third "equals" sign is " ", not " ". Simplify sqrt(–25). Simplify sqrt(–18). Simplify –sqrt(–6).
Radius of convergence Definition[edit] For a power series ƒ defined as: where cn is the nth complex coefficient, and z is a complex variable. The radius of convergence r is a nonnegative real number or ∞ such that the series converges if and diverges if In other words, the series converges if z is close enough to the center and diverges if it is too far away. Finding the radius of convergence[edit] Two cases arise. then you take certain limits and find the precise radius of convergence. Theoretical radius[edit] The radius of convergence can be found by applying the root test to the terms of the series. "lim sup" denotes the limit superior. and diverges if the distance exceeds that number; this statement is the Cauchy–Hadamard theorem. The limit involved in the ratio test is usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite. This is shown as follows. That is equivalent to Practical estimation of radius[edit] Domb–Sykes plot of the function as a function of index . by