Méthode Trachtenberg

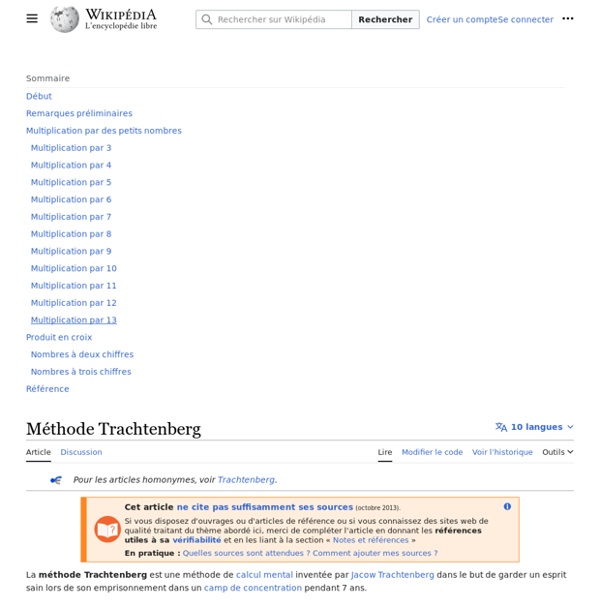
Soroban Le soroban est le boulier japonais. Caractéristiques[modifier | modifier le code] un soroban avec le nombre 987654321 Par rapport au boulier chinois, il ne comporte que le minimum de boules requises pour effectuer les opérations sur le boulier, c'est-à-dire une seule quinaire (en haut du boulier) et 4 unaires (en bas). On peut y effectuer toutes les opérations de base de l'arithmétique (addition, soustraction, multiplication, division), et même pour les experts, des extractions de racine, calcul en binaire, octal, hexadécimal et autres. Il est nécessaire de connaître ses tables d'addition ainsi que ses tables de multiplication (minimum jusqu'à 10) pour effectuer des multiplications. Efficacité[modifier | modifier le code] La technique permet d'automatiser les manipulations sur le soroban, et d'atteindre, avec de l'entrainement, des vitesses impressionnantes. Histoire[modifier | modifier le code] Introduction et évolution[modifier | modifier le code] Un boulier avec calculatrice intégrée.

DES LIVRES POUR CHANGER DE VIE par Olivier Roland Tchebychev Pafnouti Tchebychev (aussi orthographié Chebyshev, notamment dans les pays anglophones) est né le 16 mai 1821 à Okatovo (ouest de la Russie). Il est issu d'une famille militaire mais ne pourra poursuivre dans cette voie car il est né avec une jambe plus longue que l'autre. La richesse de sa famille lui permet d'avoir un précepteur à domicile, et il reçoit une bonne éducation en mathématiques et en français (son père s'est battu contre l'armée napoléonienne et souhaitait que ses enfants découvrent la culture française). Il déménage en 1832 à Moscou, où il a le tuteur ayant la meilleure réputation en mathématiques. Il entre en 1837 à l'université de Moscou. En 1841, alors qu'il commence à obtenir de bons résultats, la famine frappe la Russie et sa famille doit partir de Moscou. Tchebychev s'est intéressé aussi bien aux mathématiques fondamentales qu'appliquées. Sources :Bibmathwww.st-andrews.ac.uk

Trachtenberg system System of rapid mental calculation The Trachtenberg system is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. The rest of this article presents some methods devised by Trachtenberg. The section on addition demonstrates an effective method of checking calculations that can also be applied to multiplication. General multiplication, Trachtenberg math theory[edit] The method for general multiplication is a method to achieve multiplications with low space complexity, i.e. as few temporary results as possible to be kept in memory. times the next-to-last digit of , as well as the next-to-last digit of times the last digit of . In general, for each position in the final result, we sum for all People can learn this algorithm and thus multiply four digit numbers in their head – writing down only the final result. Example: The units digit of The first digit of the answer is . is ignored. plus

Youmatter | Comprendre pour mieux agir Machine plantigrade / Études // Études Mathématiques Mais Tche­by­shev remarqua que la courbe bleu n’est pas semblable seule­ment à la calotte d’un cham­pi­gnon, mais aussi à la trajec­toire tracée par le sabot d’un cheval! Atta­chons au méca­nisme une jambe avec un “pied”. À ses char­nières situées aux points fixes atta­chons un autre méca­nisme pareil, avec la jambe et le pied, ma déphasé d’un demi–tour par rapport au premier. Ajou­tons ensuite une copie miroir de ce méca­nisme double que nous venons de construire. Pafnutiy Lvovitch Tche­by­shev, alors qu’il était profes­seur à l’Univer­sité de Saint–Péters­bourg, a passé la plupart de son temps dans la construc­tion de méca­nismes qu’il avait inventé.

Calcul mental rapide : Ces élèves qui font mentir notre article « échecs et maths » [Vidéo] Notre article « Echecs et maths » sur le long déclin du niveau scolaire en France, a fait réagir. Notamment cette internaute, de l’école Sainte-Bernadette à Tarbes (Hautes-Pyrénées), qui nous a adressé une vidéo de ses élèves, et le résultat est juste stupéfiant. Ces conseils vous ont plu ? Cela tombe bien, l’école Sainte-Bernadette à Tarbes (Hautes-Pyrénées) doit s’agrandir. Crédit photo : DR[cc] Breizh-info.com, 2019, dépêches libres de copie et de diffusion sous réserve de mention et de lien vers la source d’origine

OpenEdition Journals Polynômes de Tchebychev Les polynômes de Tchebychev sont des familles de polynômes orthogonaux pour un produit scalaire sur ]−1,1[. Ils interviennent également dans des problèmes d'interpolation polynomiale. Polynômes de Tchebychev de première espèce Les polynômes de Tchebychev de première espèce sont les uniques polynômes (Tn)n≥0 définis sur [−1,1] par Tn(x)=cos(narccosx) ou encore Tn(cosθ)=cos(nθ). Le degré de Tn est égal à n, et son coefficient dominant est 2n−1. Polynômes de Tchebychev de seconde espèce Les polynômes de Tchebychev de seconde espèce sont les uniques polynômes (Un)n≥0 définis sur ]−1,1[ par Un(cosθ)=sin((n+1)θ)sinθ. Le degré de Un est égal à n, et son coefficient dominant est 2n. Consulter aussi...