


How Mandelbrot's fractals changed the world 18 October 2010Last updated at 14:15 By Jack Challoner Science writer Fractals have become a common sight, thanks to computer imagery In 1975, a new word came into use, when a maverick mathematician made an important discovery. So what are fractals? And why are they important? During the 1980s, people became familiar with fractals through those weird, colourful patterns made by computers. But few realise how the idea of fractals has revolutionised our understanding of the world, and how many fractal-based systems we depend upon. On 14 October 2010, the genius who coined the word - Polish-born mathematician Benoit Mandelbrot - died, aged 85, from cancer. Unfortunately, there is no definition of fractals that is both simple and accurate. The best way to get a feeling for what fractals are is to consider some examples. They are all complicated and irregular: the sort of shape that mathematicians used to shy away from in favour of regular ones, like spheres, which they could tame with equations.
Using Body Awareness For Deeper Meditation & We The Change, Personal Development for Conscious People | Exploring How Self-Improvement Plays a Role in Global Consciousness I would like to share with you a very powerful meditation technique I use called ‘body awarenes s’. Even though this practice is primarily used during meditation, I have found great use in utilizing body awareness in my every day life as well. For those of you who already have a meditation practice, I highly recommend trying the following steps. For those of you who do not currently meditate, the practice brings a great sense of peace, joy, perspective and fulfillment into your life. I highly recommend you giving it a whirl and have written two excellent pieces on ‘meditation for beginners’. How To Meditate For Beginners20 Steps for Quieting The Mind Body awareness is extremely healthy and initiates the flow of fresh oxygenated blood to body areas that usually fall below the radar of your consciousness: Using the Body The big question for beginners is: where do I focus my attention during meditation? First, it is always helpful to make your practice of meditation ‘formal’. nostrils.
The Mandelbrot Set : Good Math, Bad Math The most well-known of the fractals is the infamous Mandelbrot set. It’s one of the first things that was really studied *as a fractal*. It was discovered by Benoit Mandelbrot during his early study of fractals in the context of the complex dynamics of quadratic polynomials the 1980s, and studied in greater detail by Douady and Hubbard in the early to mid-80s. It’s a beautiful example of what makes fractals so attractive to us: it’s got an extremely simple definition; an incredibly complex structure; and it’s a rich source of amazing, beautiful images. So what is the Mandelbrot set? Take the set of functions fC(x)=x2+C where for each fC, C is a particular complex constant. * m(0,C)=fC(0) * m(i+1,C)=fC(m(i,C)) If m(i,C) doesn’t diverge (escape) towards infinity as i gets larger, then the complex number C is a member of the Mandelbrot set. If we use that definition of the Mandelbrot set, and draw the members of the set in black, we get an image like the one above.
[ wu :: fractals ] A Short And Entertaining Introduction to Fractals usually one's first response to fractals is simply this: they are beautiful! indeed, they are visually arresting, and there are many reasons why. perhaps one reason is that they exhibit extreme levels of symmetry, a property we have gravitated toward throughout human history, whether it be in our architectural designs, in our scientific theories, in our religions, or even in the facial structures of the opposite sex. another reason could be that the same self-replicative patterns can be found strewn throughout our natural universe, in vapor trails, snail shells, evergreens, cauliflowers, and snowflakes ... just to name a few. but perhaps most enticing is a reason most people would never guess -- mathematical brevity. many of these stunning patterns are governed by very simple-looking equations consisting of only a few symbols!
Mandelbrot Set - Labix Introduction These snippets compute and draw a graphic representation for the classical Mandelbrot set fractal. Results Running under pygame: Running under a Nokia 770 with pymaemo (also pygame): Running under a Nokia N70 with Python for Series 60: Code for pygame Toggle line numbers Code for Series 60 Author Gustavo Niemeyer <gustavo@niemeyer.net> CategorySnippet Benoît Mandelbrot Benoît Mandelbrot is not an artist in the usual sense of the word. He doesn’t work with oils, watercolors, pastels or colored pencils, yet he has created work of extraordinary beauty. Benoît Mandelbrot is a mathematician. He coined the term “fractal” in 1975 to describe a shape that appears similar at all levels of magnification. Fractals occur in nature. The nature of cloud formations, seemingly too complex for traditional geometry and mathematics to describe, is revealed to be an expression of fractal geometry. Mandelbrot worked with this branch of math and in the process created one of those wonderfully simple and elegant mathematical expressions, like Einstein’s “E=Mc2”, that is incredibly far reaching. The arrows on the equal sign indicate that the equation can be processed in either direction, and the result of one operation can become the start of the next, ad infinitum, in a process known as iteration.
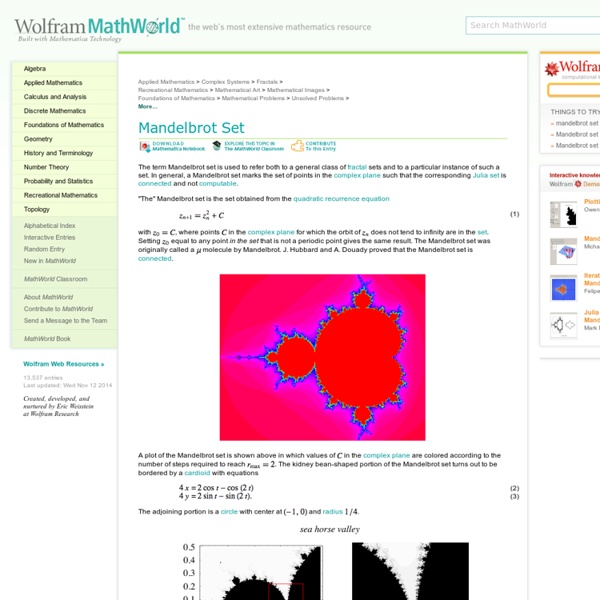
The Mandelbrot Set Understanding Mathematics by Peter Alfeld, Department of Mathematics, University of Utah The Mandelbrot Set. Note: All of the Mandelbrot pictures on this page were generated with the applet on this page! You can click on any of them to see a large version, and you can use the applet to generate those very same pictures, or similar pictures all your own! The first picture ( No1 ) shows a small part of the Mandelbrot set (which is rendered in red). List of Contents What's so special about the Mandelbrot set? What is the Mandelbrot set? z(0) = z, z(n+1) = z(n)*z(n) + z, n=0,1,2, remains bounded. You may ask, what's so special about the particular iteration (1), and why do we use complex numbers instead of real ones. Much of the fascination of the Mandelbrot set stems from the fact that an extremely simple formula like (1) gives rise to an object of such great complexity. Consider this picture ( Title ). Now, I know you already clicked on that applet! This is what you should see. Max.
Mandelbrot set from moire patterns Mandelbrot Cauliflower Mandelbrot cauliflower Shopping in October, 2006 at Volante Farm, in Needham, MA, I came across this unusual cauliflower. It reminded me of a picture I saw somewhere of a piece of the Mandelbrot set. I doubt that I can find the picture I remember. Can anyone reading this help, either by pointing me to an image, or by exploring the Mandelbrot set to find a place that looks like this? I'll post promising matches - send them to me at eb AT cs DOT umb DOT edu. Here is some of the correspondence so far. Two images I found with a Google search: from www.math.kyoto-u.ac.jp/~mitsu/gallery/M-zoom.html from www.spsu.edu/math/edwards/mandel/manpics/otherpics.htm
Mystery of the Real 3D Mandelbrot Fractal They're all very nice, but imagine such pictures in three dimensions, with all the advantages that 3D can allow such as parallax, perspective, and richer detail along with subtle light sourcing, shadows, and reflections. And actually, it turns out there are quite a few '3D' Mandelbot pics out there if you look..... Mandelbrot Flavours .....But are they the real McCoy, or just pale imitations? Existence of 3D Mandelbrot set? No, the thing I've been looking for has the essential characteristics of the traditional 2D Mandelbrot, but extended to 3 dimensions. We can try and guess the overall shape's outline too. Below is a third visualization using a formula I created based on pseudo 3 dimensional complex numbers (and nicely rendered by Thomas Ludwig). Also see Thomas' amazing metallic render of the same design. But even more than the overall shape, like the 2D Mandelbrot, the most incredible visuals would be witnessed once you've zoomed in to the hypothetical 3D Mandelbrot. External links:
Fullscreen Gigapan Viewer: Mandelbrot Fractal Want to add this gigapan to your favorites? or now. now to add this Gigapan to a group gallery. now to add this Gigapan to a gallery. About This Gigapan Toggle Taken by Peter Explore score Size 7.50 Gigapixels Views Date added Apr 29, 2011 Date taken Categories Galleries Experimental Gigapixel Images Competitions Tags mandelbrot, fractal Description Took longer to put it together than to render lol, it created a 60GB temp file in photoshop when I had it all loaded xD Where in the World is this GigaPan? Toggle