Geometric Sculpture of George W. Hart, mathematical sculptor

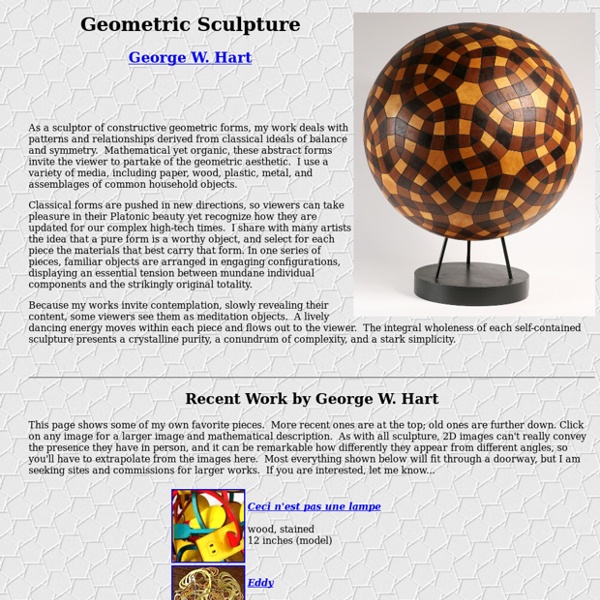
George W. Hart As a sculptor of constructive geometric forms, my work deals with patterns and relationships derived from classical ideals of balance and symmetry. Mathematical yet organic, these abstract forms invite the viewer to partake of the geometric aesthetic. I use a variety of media, including paper, wood, plastic, metal, and assemblages of common household objects. Classical forms are pushed in new directions, so viewers can take pleasure in their Platonic beauty yet recognize how they are updated for our complex high-tech times. Because my works invite contemplation, slowly revealing their content, some viewers see them as meditation objects. This page shows some of my own favorite pieces. Public and Corporate Artworks University of London (2006) Massachusettes Institute of Technology (2003) Stony Brook University Northport Public Library (1999) Long Island Museum of Science and Technology (1999) U.C. More

Paper Sculpture | technogad February 17, 2008 Kirsten Hassenfeld sculptures made from intricate paper cut outs, and so intricate at such scale… Click on the link to see more. Extract from bellwether Like this: Like Loading... George Glazer Gallery - Antique Botanical Prints - 8 Ladies Slipper Orchid (Cypripedium) Botanical Prints Jeanne Koch (after) G. Severeyns (chromolithographer) Ladies Slipper Orchid (Cypripedium) Botanical Prints from Les Cypripediées A. Godefroy-Lebeuf & Brown, Argenteuil, France: December 15, 1888 Chromolithographs 13.25 x 10.5 inches, overall Pair of Horizontal Orchids: $800, the pair Vertical Orchids: $2,400, set of 6 Botanical studies of ladies slipper orchids (genus Cypripedium). This rare set was issued in 1888, about the same time as other popular series of orchid periodicals when Victorian orchidomania spread throughout Europe. Les Cypripediées was dedicated to the orchid cultivator J. G. A. Condition: Generally very good with the usual overall light toning, wear, soiling, soft creases. Reference: Blunt, Wilfred, rev. by Stearn, William T.