

Pitagora formula. Triangolo. Un triangolo in Geometria è un poligono formato da tre lati e tre angoli, ed in particolare è il tipo di poligono con il minor numero possibile di lati che si possa costruire.
Qui di seguito vi proponiamo una sintesi completa sul triangolo, ed in particolare tutte le definizioni da sapere, le proprietà che caratterizzano i triangoli e le formule del triangolo qualsiasi. Nota bene: nel corso di questo formulario presenteremo la classificazione dei triangoli e vedremo che è possibile distinguere tra diversi tipi di triangoli in base ai lati e agli angoli. Tra queste tipologie alcune ammettono ulteriori formule e proprietà, che tratteremo nei formulari correlati (rettangolo, isoscele, equilatero); per tutti gli altri tipi di triangoli (con particolare riferimento al triangolo scaleno) le uniche formule che valgono in generale sono quelle che potete leggere qui sotto. Teorema di Pitagora - Formule e Spiegazione. Intorno al 2900 a.C gli antichi Egizi scoprirono che per alcune terne di numeri, a, b, c, corrispondenti alle misure dei lati di un triangolo rettangolo si verifica che: Più tardi, nel VI secolo a.C.
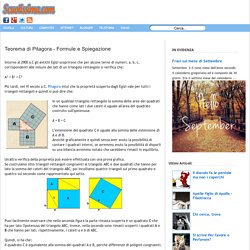
Pitagora intuì che la proprietà scoperta dagli Egizi vale per tutti i triangoli rettangoli e quindi si può dire che: In un qualsiasi triangolo rettangolo la somma delle aree dei quadrati che hanno come lati i due cateti è uguale all'area del quadrato costruito sull'ipotenusa: L’estensione del quadrato C è uguale alla somma delle estensione di A e di B. Anziché graficamente e quindi senza aver avuto la possibilità di contare i quadrati interni, se avremmo avuto la possibilità di disporli su una bilancia avremmo notato che sarebbero rimasti in equilibrio. Un'altra verifica della proprietà può essere effettuata con una prova grafica. Quindi, si ha che: Il quadrato C è equivalente alla somma dei quadrati A e B, perché differenze di poligoni congruenti.
Pythagora Switch. FILOSOFIA 3 - Pitagora (parte 1) Pythagorean Theorem and its many proofs. Professor R.

Smullyan in his book 5000 B.C. and Other Philosophical Fantasies tells of an experiment he ran in one of his geometry classes. He drew a right triangle on the board with squares on the hypotenuse and legs and observed the fact the the square on the hypotenuse had a larger area than either of the other two squares. Then he asked, "Suppose these three squares were made of beaten gold, and you were offered either the one large square or the two small squares. Which would you choose? " Interestingly enough, about half the class opted for the one large square and half for the two small squares. The Pythagorean (or Pythagoras') Theorem is the statement that the sum of (the areas of) the two small squares equals (the area of) the big one. In algebraic terms, a² + b² = c² where c is the hypotenuse while a and b are the legs of the triangle. The theorem is of fundamental importance in Euclidean Geometry where it serves as a basis for the definition of distance between two points.
R. Pythagoras Theorem. Pythagoras Over 2000 years ago there was an amazing discovery about triangles: When a triangle has a right angle (90°) ... ... and squares are made on each of the three sides, ... © 2017 MathsIsFun.com v0.8 ... then the biggest square has the exact same area as the other two squares put together! It is called "Pythagoras' Theorem" and can be written in one short equation: a2 + b2 = c2 Note: c is the longest side of the triangle a and b are the other two sides Definition The longest side of the triangle is called the "hypotenuse", so the formal definition is: Pythagoras - Wikipedia. 6th century BC Ionian Greek philosopher and mystic Pythagoras of Samos[a] (c. 570 – c. 495 BC)[b] was an ancient Ionian Greek philosopher and the eponymous founder of Pythagoreanism.
His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, Western philosophy. Knowledge of his life is clouded by legend, but he appears to have been the son of Mnesarchus, a gem-engraver on the island of Samos. Modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, ascetic lifestyle. This lifestyle entailed a number of dietary prohibitions, traditionally said to have included vegetarianism, although modern scholars doubt that he ever advocated for complete vegetarianism.
Biographical sources Life Early life Alleged travels In Croton Death .