

Activités autour de la trigonométrie. UN GRAND REMERCIEMENT AUX WEBMASTERS DES SITES SUIVANTS POUR LEURS INFORMATIONS ET LEURS IMAGES « LIBRES » sans brevet : Merci aux enseignants de l’académie de Clermont-Ferrand pour leur excellente banque de données mise à la disposition des enseignants, tout particulièrement pour l’article sur la trigonométrie de Jean Philippe Darras.
Merci à Daniel Joly pour son bel article sur les ondes radio et pour l’autorisation de publier une image de son site. Un grand merci à Wikimedia Commons pour toutes ces images libres qui m’ont permis de réaliser le diaporama sur l’histoire de la trigonométrie. Merci à Wikipédia pour l’histoire des mathématiciens arabes. Merci au webmaster de Chronomath pour son excellent site. 1. Activité de découverte 2. Cette figure permet de faire apparaître la courbe sinusoïdale à partir d’un cercle : Créé avec GeoGebra 3. Histoire de la trigonométrie Au IIIe siècle avant J. C’est en Grèce, à la même époque, que la trigonométrie allait vraiment commencer. . 4. Sinus, cosinus et tangente d'un nombre réel. Trianglesisometriques.pdf. La trigonométrie. Quand on parle de trigonométrie, on associe nécessairement le mot aux fonctions cosinus, vues en 4e, puis sinus et tangente, vues en 3e pour le calcul de longueurs ou d’angles dans le triangle.
Aujourd’hui, l’usage de la calculatrice est incontournable lorsqu’on applique ces fonctions. Mais si l’on remonte à la fin des années 70, les collégiens ne disposaient pas encore de calculatrice et devaient se munir de tables trigonométriques pour effectuer les calculs. Le mot vient du grec "trigone" (triangle) et "metron" (mesure). Dans l’Encyclopédie (1751), Jean le Rond d’Alembert (1717 ; 1783) définit la trigonométrie comme « l’art de trouver les parties inconnues d’un triangle par le moyen de celles qu’on connaît ». C’est bien la démarche qui est demandée aux élèves du collège.
Il faut remonter jusqu’aux babyloniens, 2000 ans avant notre ère, pour trouver les premières traces de tables de données astronomiques. Le grec Claude Ptolémée (90? Pour exemple, en voici quelques-unes : Géométrie. Histoire des maths. Mathematics ! - Download free content from Université Pierre et Marie Curie. Loi des sinus. Un article de Wikipédia, l'encyclopédie libre.
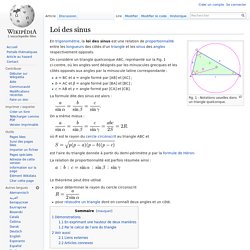
Fig. 1 - Notations usuelles dans un triangle quelconque. On considère un triangle quelconque ABC, représenté sur la Fig. 1 ci-contre, où les angles sont désignés par les minuscules grecques et les côtés opposés aux angles par la minuscule latine correspondante : a = BC et α = angle formé par [AB] et [AC] ;b = AC et β = angle formé par [BA] et [BC] ;c = AB et γ = angle formé par [CA] et [CB]. La formule dite des sinus est alors : On a même mieux : où R est le rayon du cercle circonscrit au triangle ABC et est l'aire du triangle donnée à partir du demi-périmètre p par la formule de Héron. Loi des cosinus. Un article de Wikipédia, l'encyclopédie libre.
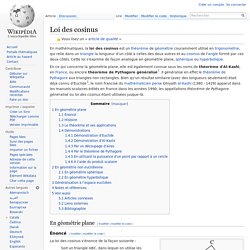
En mathématiques, la loi des cosinus est un théorème de géométrie couramment utilisé en trigonométrie, qui relie dans un triangle la longueur d'un côté à celles des deux autres et au cosinus de l'angle formé par ces deux côtés. Cette loi s'exprime de façon analogue en géométrie plane, sphérique ou hyperbolique. En ce qui concerne la géométrie plane, elle est également connue sous les noms de théorème d'Al-Kashi, en France, ou encore théorème de Pythagore généralisé[1]. Il généralise en effet le théorème de Pythagore aux triangles non rectangles. Bien qu'un résultat similaire (avec des longueurs seulement) était déjà connu d'Euclide[2], le nom francisé du mathématicien perse Ghiyath al-Kashi (1380 - 1429) apparut dans les manuels scolaires édités en France dans les années 1990, les appellations théorème de Pythagore généralisé ou loi des cosinus étant utilisées jusque-là.
Trigonometrie. Que signifie le mot "trigonométrie "?
Pourquoi la trigonométrie ? Qui a inventé la trigonométrie ? Comment obtenir les tables de trigonométrie ? Le sinus (noté sin au XVIIe siècle ) La trigonométrie. Quelques notes historiques sur l’introduction de la trigonométrie et en particulier du radian. Quelques notes historiques sur l’introduction de la trigonométrie et en particulier du radian.

La trigonométrie à travers les siècles (d’après la "Petite histoire de la trigonométrie" de Jean Lefort, parue dans l’Ouvert de juin 98) Très tôt dans l’histoire de l’humanité s’est inscrit le désir de mesurer des phénomènes apparemment réguliers, comme le retour des saisons, le déplacement des planètes. Mesurer dans le but de prévoir et ainsi apprivoiser ces phénomènes qui, croyaient-ils, influençaient leur vie. Or, noter la position des étoiles sur la voûte céleste ne se fait correctement qu’au moyen des angles, notion qui apparaît déjà dans les premiers écrits des Sumériens connus ; comme les étoiles (se décalent chaque jour) font un tour complet en une année, le peuple Sumer choisit la 360e partie du cercle pour des raisons qui tiennent à la fois à la durée de l’année et à leur système de numération de base 60. Le degré, unité sexagésimale, est né ! Origine du mot " sinus " :