Le Nombre d'Or. Nombre d'or. Un article de Wikipédia, l'encyclopédie libre.
Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . Il utilise également la racine carrée de 5 comme rapport.
IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d'or. Le Nombre d'or. Le 2 septembre 2019 - Ecrit par Fernando Corbalán Cet article a été écrit en partenariat avec L’Institut Henri Poincaré Lire l'article en En 2013, l’Institut Henri Poincaré et Images des Mathématiques ont uni leurs efforts pour superviser la réédition de la collection Le monde est mathématique, publiée par RBA en partenariat avec Le Monde.
En 40 ouvrages, cette collection de qualité, issue d’un projet collectif de mathématiciens espagnols, vise à présenter, à travers une grande variété de points de vue, de multiples facettes des sciences mathématiques, sous un aspect historique, humain, social, technique, culturel ... Suite de Fibonacci. Un article de Wikipédia, l'encyclopédie libre.

Elle doit son nom à Leonardo Fibonacci qui, dans un problème récréatif posé dans l'ouvrage Liber abaci publié en 1202, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Croissance de population des lapins selon une suite de Fibonacci Présentation mathématique[modifier | modifier le code] Formule de récurrence[modifier | modifier le code]
Leonardo Fibonacci. Un article de Wikipédia, l'encyclopédie libre.
Leonardo Fibonacci Statue de Léonard de Pise, dans sa ville natale Leonardo Fibonacci (v. 1175 à Pise, Italie - v. 1250) est un mathématicien italien. Fibonacci Sequence. The Fibonacci Sequence is the series of numbers: The next number is found by adding up the two numbers before it.

The 2 is found by adding the two numbers before it (1+1) Similarly, the 3 is found by adding the two numbers before it (1+2), And the 5 is (2+3), and so on! Example: the next number in the sequence above is 21+34 = 55 It is that simple! Here is a longer list: Can you figure out the next few numbers? Makes A Spiral When we make squares with those widths, we get a nice spiral: Do you see how the squares fit neatly together? The Rule The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series). First, the terms are numbered from 0 onwards like this: So term number 6 is called x6 (which equals 8). Pi.
Un article de Wikipédia, l'encyclopédie libre.
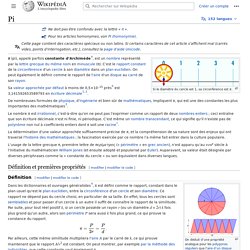
Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Si le diamètre du cercle est 1, sa circonférence est π. Sa valeur approchée par défaut à moins de 0,5×10–15 près[2] est 3,141 592 653 589 793 en écriture décimale[3],[4]. De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques[5].
Nombre premier. Un article de Wikipédia, l'encyclopédie libre. Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Ainsi, 1 n'est pas premier car il n'a qu'un seul diviseur entier positif ; 0 non plus car il est divisible par tous les entiers positifs. Par opposition, un nombre non nul produit de deux nombres entiers différents de 1 est dit composé. Par exemple 6 = 2 × 3 est composé, tout comme 21 = 3 × 7 ou 7 × 3, mais 11 est premier car 1 et 11 sont les seuls diviseurs de 11. De telles listes de nombres premiers inférieurs à une borne donnée, ou compris entre deux bornes, peuvent être obtenues grâce à diverses méthodes de calcul.
La notion de nombre premier est une notion de base en arithmétique élémentaire : le théorème fondamental de l'arithmétique assure qu'un nombre composé est factorisable en un produit de nombres premiers, et que cette factorisation est unique à l'ordre des facteurs près. Notes :(*) et . Prime number. A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself.