

U27 Ass Example. DO NOT USE. Playlist of my vids for this assignment. Tensile Test. Stress strain curve explained with tensile test. Stress/ Strain/ Linear Expansion Content. Axial Stress in a bar due to temp change and clamping force. Axial stress in a series compound bar. Stress in a parallel compound bar due to axial load. Built from branch 'tiddlywiki-com' at commit f49c55fe3c6c250fb46372b43d6b8f73fa532790 of at 2019-08-09 14:49:54 UTC Kookma plugin library is a set of plugins, themes, and scripts, to extend functionality and add new features to Tiddlywiki.

For detail information visit the library at [[GitHub| It is recommended to backup your data before installing any plugin, theme, or script. To use in other wikis, drag and drop this link to those wikis: [[Kookma Plugin Library|$:/config/KookmaPluginLibrary]] $:/core/ui/EditTemplate/tags ~WikiLabs plugin library latest version! Stress in a Parallel Compound Bar due to Thermal Expansion Worked Example. Built from branch 'tiddlywiki-com' at commit f49c55fe3c6c250fb46372b43d6b8f73fa532790 of at 2019-08-09 14:49:54 UTC Kookma plugin library is a set of plugins, themes, and scripts, to extend functionality and add new features to Tiddlywiki.

For detail information visit the library at [[GitHub| It is recommended to backup your data before installing any plugin, theme, or script. To use in other wikis, drag and drop this link to those wikis: [[Kookma Plugin Library|$:/config/KookmaPluginLibrary]] Shear stress in a lap joint and butt joint. Built from branch 'tiddlywiki-com' at commit f49c55fe3c6c250fb46372b43d6b8f73fa532790 of at 2019-08-09 14:49:54 UTC $:/core/ui/EditTemplate/tags ~WikiLabs plugin library latest version!

The Spread Sheet. Spreadsheet set up and explained for first bit of Pass. AWC DA6 BeamFormulas 0710. Moment table. What next. What next next. Area Moment of Inertia - Typical Cross Sections I. Universal RSJ Steel Beams. Buy Universal RSJ Steel Beams online from metals4U or phone on 01937 534318 for a quick delivery.
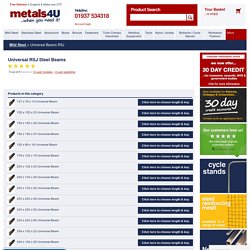
We stock a wide range of sizes all available in standard lengths up to 6000mm or custom cut to your required dimension. The RSJs are all produced to BS 4 part 1 BE EN 10025 S275JR which is the new European structural steel standard meaning it has a minimum yield strength (reh) of 235 MPa at16mm and a Longitudinal Charpy V-notch impacts of 27J at 20 degrees centigrade Our RSJ Steel Beams are normally delivered pre-painted in Red Oxide. Red Oxide primer is an anti-corrosion coating to help prevent the formation of rust, ensuring long term durability. Should you require a beam untreated please contact us on 01937 534318 to specify your requirements and we will be able to help.
Rolled Steel Joists or I Beams as they sometimes called are rolled from a single piece of structural steel to maintain structural integrity. Diagram to go with 'Metals 4 U' Website. Universal RSJ Beams (I-Beam) Bending Equation Derivation With Simple Step By Step Explanation. Bending theory is also known as flexure theory is defined as the axial deformation of the beam due to external load that is applied perpendicularly to a longitudinal axis which finds application in applied mechanics.
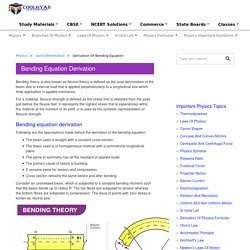
For a material, flexural strength is defined as the stress that is obtained from the yield just before the flexure test. It represents the highest stress that is experienced within the material at the moment of its yield. 𝜎 is used as the symbolic representation of flexural strength. Following are the assumptions made before the derivation of the bending equation: The beam used is straight with a constant cross-section.The beam used is of homogeneous material with a symmetrical longitudinal plane.The plane of symmetry has all the resultant of applied loads.The primary cause of failure is buckling.E remains same for tension and compression.Cross-section remains the same before and after bending.
Strain in fibre AB is the ratio of change in length to original length. DERIVATION OF BEAM BENDING EQUATION - Mechanical engineering concepts and principles. Now we are going ahead to start new topic i.e. derivation of flexure formula or bending equation for pure bending in the strength of material with the help of this post.

Let us go ahead step by step for easy understanding, however if there is any issue we can discuss it in comment box which is provided below this post. Let us consider one structural member such as beam with rectangular cross section, we can select any type of cross section for beam but we have considered here that following beam has rectangular cross section. First of all we will find here the expression for bending stress in a layer of the beam subjected to pure bending and aftre that we will understand the concept of moment of resistance and once we will have these two information, we can easily secure the bending equation or flexure formula for beams.
So let us first find out the expression for bending stress acting on a layer of the beam subjected to pure bending. Calculating the Moment of Inertia of a Beam Section. How to Calculate the Moment of Inertia of a Beam Section(Second Moment of Area) Before we find the moment of inertia (or second moment of area) of a beam section, its centroid (or center of mass) must be known.
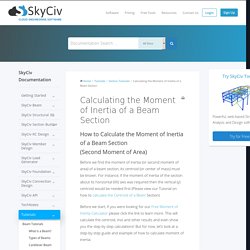
For instance, if the moment of inertia of the section about its horizontal (XX) axis was required then the vertical (y) centroid would be needed first (Please view our Tutorial on how to calculate the Centroid of a Beam Section). Before we start, if you were looking for our Free Moment of Inertia Calculator please click the link to learn more. This will calculate the centroid, moi and other results and even show you the step by step calculations! SkyCiv Cloud Structural Analysis Software.
'Blue Book' home - Blue Book - Steel for Life. Jeff Hanson. Solids: Lesson 49 - Introduction to Beam Design Example Problem. Old Notes 1.1. Thermal Expansion Stress – Strength of Materials Supplement for Power Engineering. Thermal Expansion Learning Objectives At the end of this section you should be able to calculate problems involving Unrestricted thermal expansionRestricted thermal expansion All materials subject to a temperature change will expand or contract proportional with their length and temperature difference.
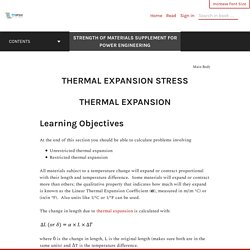
Some materials will expand or contract more than others; the qualitative property that indicates how much will they expand is known as the Linear Thermal Expansion Coefficient (α), measured in m/(m ºC) or (in/in ºF). The change in length due to thermal expansion is calculated with: where δ is the change in length, L is the original length (makes sure both are in the same units) and ΔT is the temperature difference. For example if steel has a thermal expansion coefficient of 11.7×10-6 1/ºC it means that a 1 m long bar subject to a temperature increase of 1ºC will expand 11.7×10-6 m, or 0.0117 mm.
Pipelines expansion Pipe cold springing. Solution to Problem 266 Thermal Stress. Second moment of area - I-Beam (W-section) - calculator - fxSolver. An I-beam, also known as H-beam, W-beam (for “wide flange”), Universal Beam (UB), Rolled Steel Joist (RSJ), or double-T (especially in Polish, Bulgarian, Spanish, Italian and German), is a beam with an I- or H-shaped cross-section.
The horizontal elements of the “I” are known as flanges, while the vertical element is termed the “web”. I-beams are usually made of structural steel and are used in construction and civil engineering. The web resists shear forces, while the flanges resist most of the bending moment experienced by the beam. Beam theory shows that the I-shaped section is a very efficient form for carrying both bending and shear loads in the plane of the web. On the other hand, the cross-section has a reduced capacity in the transverse direction, and is also inefficient in carrying torsion, for which hollow structural sections are often preferred.