

Introduction to Binary Numbers. How Computers Store Numbers Computer systems are constructed of digital electronics.

That means that their electronic circuits can exist in only one of two states: on or off. Most computer electronics use voltage levels to indicate their present state. For example, a transistor with five volts would be considered "on", while a transistor with no voltage would be considered "off. " Not all computer hardware uses voltage, however. These patterns of "on" and "off" stored inside the computer are used to encode numbers using the binary number system. The binary number system is a method of storing ordinary numbers such as 42 or 365 as patterns of 1's and 0's. How Binary Works The decimal number system that people use every day contains ten digits, 0 through 9. Another way to make this clear is to write decimal numbers in expanded notation. 365, for example, is equal to 3×100 + 6×10 + 5×1. 1032 is equal to 1×1000 + 0×100 + 3×10 + 2×1.
Not so Horrible Hexadecimal! Game. Hexadecimal Drum Machine. Create your own rhythms!

And learn about binary, decimal and hexadecimal numbers, too. Instructions: Click on the lights next to each type of drum, or change the Rhythm Number. (Hint: if you like a rhythm, save the rhythm number - you can come back and re-enter it later.) Also read the explanation below. Explanation There are 4 instruments (HiHat, Snare, Tom and Base). If you write down "1" for Play and "0" for Don't Play, then you could have a combination like HiHat and Tom being "1010", or HiHat and Base being "1001".
So, at any point in time these are the possible combinations (1=Play, 0=Don't Play): In the column next to the Binary Numbers are the matching Decimal Numbers and then the Hexadecimal Numbers. Hexadecimal Numbers The Hexadecimal numbers are interesting. So a single Hexadecimal digit can show 16 different values instead of the normal 10. How does this help? It is a more natural way to show anything that has 16 combinations ... in other words it is "neat". Computers. Number Systems: An Introduction to Binary, Hexadecimal, and More. Ever see crazy binary numbers and wonder what they meant?
Ever see numbers with letters mixed in and wonder what is going on? You'll find out all of this and more in this article. Hexadecimal doesn't have to be scary. (Thanks to the ReBoot Wiki for the thumbnail image.) Tag binary - Test Your Knowledge. BINARY AND HEXADECIMAL. Let's learn to count...
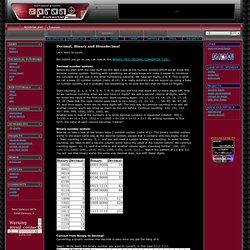
But before you go on you can look at this BINARY, HEX, DECIMAL CONVERTER TOOL! Decimal number system: Before we start with the new stuff we will take a look at the number system which we all know the decimal number system. Starting with something we already know will make it easier to introduce the concepts we will use in the other numbering systems. We have ten digits, 0 to 9. This is what we call a base 10 number system (radix of 10). Start counting: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and you will find that there are no more digits left. Binary number system: Now let us take a look at the binary base 2 number system (radix of 2). Convert from Binary to Decimal: Converting a binary number into decimal is easy once you get the hang of it.
Step1: Write down the binary number you want to convert, in this case 1111 1111. Concider the decimal number 255 = 1111 1111 in the table below: Concider the decimal number 169 = 1010 1001 in the table below: Binary, Decimal and Hexadecimal Numbers. Decimals To understand Binary and Hexadecimal numbers, it is best to know how Decimal Numbers work.

Every digit in a decimal number has a "position", and the decimal point helps us to know which position is which. The position just to the left of the point is the "Units" position. Every position further to the left is 10 times bigger, and every position further to the right is 10 times smaller: Now, this is just a way of writing down a value.
Hexadecimal Color Tutorial:1. Various alphabets with numerological values (gematria) Numeric Systems Home Page. Undefined If it weren't for this bulky title, this page would load in a good 5 seconds!

And no, this doesn't mean I'm getting rid of it. A. What are numeric systems? B. A. Glad you asked. Ancient Numeric Systems These numeric systems gave birth to our own. Modern Numeric Systems What we use today. Why do we use the base 10, you ask? So how does it all work? Representing this graphically, we'd have: As we observe, each column header's value equals 10 times the place to the right of it.
B. The binary system has a base 2, which means each column's value equals 2 times the value of the one to the right, starting with the rightmost digit, which equals 1.