

E8 lattice. The norm[1] of the E8 lattice (divided by 2) is a positive definite even unimodular quadratic form in 8 variables, and conversely such a quadratic form can be used to construct a positive-definite, even, unimodular lattice of rank 8.
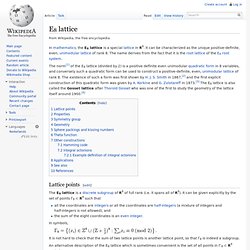
The existence of such a form was first shown by H. J. S. Smith in 1867,[2] and the first explicit construction of this quadratic form was given by A. Korkine and G. Lattice points[edit] Eisenstein prime. Small Eisenstein primes.
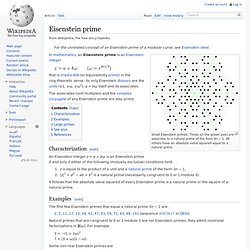
Those on the green axes are associate to a natural prime of the form 3n − 1. All others have an absolute value squared equal to a natural prime. Euler's totient function. The first thousand values of In number theory, Euler's totient or phi function, φ(n), is an arithmetic function that counts the totatives of n, that is, the positive integers less than or equal to n that are relatively prime to n.
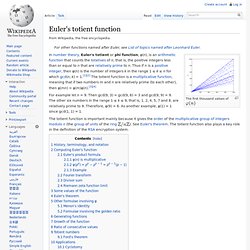
Thus if n is a positive integer, then φ(n) is the number of integers k in the range 1 ≤ k ≤ n for which gcd(n, k) = 1.[1][2] The totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime (to each other), then φ(mn) = φ(m)φ(n).[3][4] For example let n = 9. Then gcd(9, 3) = gcd(9, 6) = 3 and gcd(9, 9) = 9. Erdős–Borwein constant.
By definition it is: which is approximately 1.60669 51524 15291 763… (sequence A065442 in OEIS).
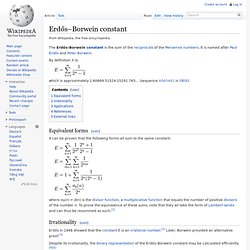
Equivalent forms[edit] It can be proven that the following forms all sum to the same constant: Palindromic prime. A palindromic prime (sometimes called a palprime) is a prime number that is also a palindromic number.
Palindromicity depends on the base of the numbering system and its writing conventions, while primality is independent of such concerns. The first few decimal palindromic primes are: Except for 11, all palindromic primes have an odd number of digits, because the divisibility test for 11 tells us that every palindromic number with an even number of digits is a multiple of 11. It is not known if there are infinitely many palindromic primes in base 10. The largest known as of March 2014[update] is It was found in 2014 by David Broadhurst. Euler's totient function.
Modular arithmetic. Time-keeping on this clock uses arithmetic modulo 12.
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value—the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801. A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two 12-hour periods.
If the time is 7:00 now, then 8 hours later it will be 3:00. Usual addition would suggest that the later time should be 7 + 8 = 15, but this is not the answer because clock time "wraps around" every 12 hours; in 12-hour time, there is no "15 o'clock". For a positive integer n, two integers a and b are said to be congruent modulo n, and written as History[edit] Congruence relation[edit] For example, because 38 − 14 = 24, which is a multiple of 12.
The same rule holds for negative values: Equivalently, and by are the same. If then: Remainders[edit] where. Quadratic reciprocity. In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers.
There are a number of equivalent statements of the theorem. Although the law can be used to tell whether any quadratic equation modulo a prime number has a solution, it does not provide any help at all for actually finding the solution. (The article on quadratic residues discusses algorithms for this.) The theorem was conjectured by Euler and Legendre and first proven by Gauss.[1] He refers to it as the "fundamental theorem" in the Disquisitiones Arithmeticae and his papers, writing The fundamental theorem must certainly be regarded as one of the most elegant of its type.
Privately he referred to it as the "golden theorem. Quadratic residue. In number theory, an integer q is called a quadratic residue modulo n if it is congruent to a perfect square modulo n; i.e., if there exists an integer x such that: Otherwise, q is called a quadratic nonresidue modulo n.
Originally an abstract mathematical concept from the branch of number theory known as modular arithmetic, quadratic residues are now used in applications ranging from acoustical engineering to cryptography and the factoring of large numbers. History, conventions, and elementary facts[edit] Fermat, Euler, Lagrange, Legendre, and other number theorists of the 17th and 18th centuries proved some theorems[1] and made some conjectures[2] about quadratic residues, but the first systematic treatment is § IV of Gauss's Disquisitiones Arithmeticae (1801). Article 95 introduces the terminology "quadratic residue" and "quadratic nonresidue", and states that, if the context makes it clear, the adjective "quadratic" may be dropped.
Jacobi symbol.