

Proportional Relationships (Common Core Standards 7.RP.2, 7.RP.2.a-d) This page describes in detail how to read the graph of proportional quantities.
Directly proportional, or varying directly are other terms that mean proportional, or that y=kx for constant of proportionality k and proportional quantities x and y. Notice that k is the slope of the graph of proportional quantities x and y. The point (0,0) will always be on the graph of proportional quantities x and y. Grade7commoncoremath - Unit 1 Ratios and Proportional Relationships. Unit 2: Ratios and Proportional Relationships (7.RP)Big Ideas:Developing understanding of and applying proportional reasoning:Students extend their understanding of ratios and develop understanding of proportionality to solve single- and multi-step problems.
Students use their understanding of ratios and proportionality to solve a wide variety of percent problems, including those involving discounts, interest, taxes, tips, and percent increase or decrease. Students solve problems about scale drawings by relating corresponding lengths between the objects or by using the fact that relationships of lengths within an object are preserved in similar objects.
Students graph proportional relationships and understand the unit rate informally as a measure of the steepness of the related line, called the slope.
7.RP.2. 7.RP.1. 7.RP - GA. 4mula Fun! :): More Proportion Help. WKU stands for Word Ratio, Known Ratio Unknown Ratio.
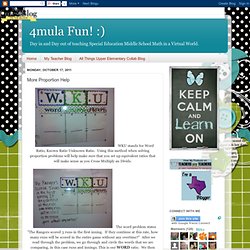
Using this method when solving proportion problems will help make sure that you set up equivalent ratios that will make sense as you Cross Multiply an Divide. The word problem states "The Rangers scored 3 runs in the first inning. If they continue at this rate, how many runs will be scored in the entire game without any overtime? " After we read through the problem, we go through and circle the words that we are comparing, in this case runs and innings. Glowing Rectangles. People spend lots of time staring at their screens (glowing rectangles). Kids spend hours each day using television, computers, mobile devices and so on.
Use that interest to motivate your student’s analysis of screen ratios. Getty Images.