

Homework HELP!; Ch.7-6; 2012 Holt McDougal Algebra 1. Factoring Checker. Factor by grouping and factoring completely. Factoring polynomials by grouping. 7-6; Example 1; ALGEBRA I Holt McDougal 2012- Lesson Tutorial Videos. 7-6; Example 2; ALGEBRA I Holt McDougal 2012- Lesson Tutorial Videos. 7-6; Example 3; ALGEBRA I Holt McDougal 2012- Lesson Tutorial Videos. Factor by grouping worksheet. Purple Math - Simple Polynomial Factoring. Simple Polynomial Factoring (page 2 of 3) Sections: Simple factoring, Factoring "in pairs" Factor x2y3 + xy I can factor an "x" and a "y" out of each term: x2y3 = xy(x1y2) = xy(xy2) and xy = xy(1). x2y3 + xy = xy( ) = xy(xy2 ) = xy(xy2 + 1) Remember: When "nothing" is left after factoring, a "1" is left behind in the parentheses.
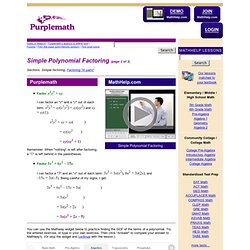
Factor 3x3 + 6x2 – 15x. I can factor a "3" and an "x" out of each term: 3x3 = 3x(x2), 6x2 = 3x(2x), and –15x = 3x(–5). 3x3 + 6x2 – 15x = 3x( ) = 3x(x2 ) = 3x(x2 + 2x ) = 3x(x2 + 2x – 5) You can use the Mathway widget below to practice finding the GCF of the terms of a polynomial. (Clicking on "View Steps" on the widget's answer screen will take you to the Mathway site, where you can register for a free seven-day trial of the software.) Factor 2(x – y) – b(x – y). This may look different from what I've done above, but really it's not. First, I'll take the common factor out front: Purple Math - A Special Case: Factoring "In Pairs"
A Special Case: Factoring "In Pairs" (page 3 of 3) Sections: Simple factoring, Factoring "in pairs" There is one special case for factoring that you may or may not need, depending upon how your book is structured and how your instructor intends to teach factoring quadratics.
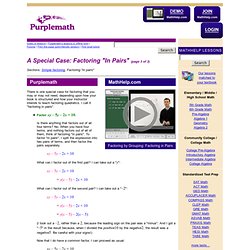
I call it "factoring in pairs". Factor xy – 5y – 2x + 10. Is there anything that factors out of all four terms? Xy – 5y – 2x + 10 What can I factor out of the first pair? = y(x – 5) – 2x + 10 What can I factor out of the second pair? = y(x – 5) – 2(x – 5) (I took out a –2, rather than a 2, because the leading sign on the pair was a "minus". Now that I do have a common factor, I can proceed as usual: = (x – 5)(y – 2) Factoring "in pairs" is most commonly used to introduce factoring quadratics.