

Les Puissances de 10. Balance du watt. Un article de Wikipédia, l'encyclopédie libre.
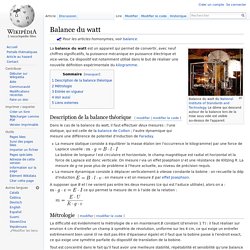
Pour les articles homonymes, voir balance. La balance du watt est un appareil qui permet de convertir, avec neuf chiffres significatifs, la puissance mécanique en puissance électrique et vice-versa. Ce dispositif est notamment utilisé dans le but de réaliser une nouvelle définition expérimentale du kilogramme. Théorème de Thalès. Configuration possible du théorème de Thalès : les droites (BC) et (DE) sont parallèles donc les triangles ADE et ABC sont semblables et les longueurs AD, DE, EA sont proportionnelles aux longueurs AB, BC et CA.
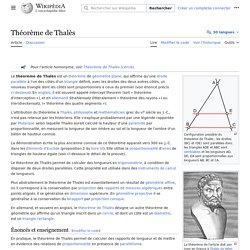
Le théorème de Thalès est un théorème de géométrie qui affirme que, dans un plan, à partir d'un triangle, une droite parallèle à l'un des côtés définit avec les droites des deux autres côtés un nouveau triangle, semblable au premier (voir énoncé précis ci-dessous). En anglais, il est connu sous le nom de intercept theorem (soit « théorème d'interception ») ; en allemand, il est appelé Strahlensatz, c'est-à-dire « théorème des rayons ». Le théorème de Thalès se généralise en dimension supérieure.
InscrireCarreFicheProf.pdf. Telechargez le zoom métiers maths. Figures Dynamiques. Mathématiques - Tableur au collège. Utilisation de la calculatrice. Références : circulaire n°99-186 du 16 novembre 1999 publiée au Bulletin officiel n°42 du 25 novembre 1999.
La présente circulaire définit les conditions d'usage des calculatrices dans les examens et concours organisés par le ministère de l'Éducation nationale et dans les concours de recrutement des personnels enseignants. La maîtrise de l'usage des calculatrices représente un objectif important pour la formation de l'ensemble des élèves car elle constitue un outil efficace dans le cadre de leurs études et dans la vie professionnelle, économique et sociale.C'est pourquoi leur utilisation est prévue dans de nombreux programmes d'enseignement et leur emploi doit être largement autorisé aux examens et concours.
Le matériel autorisé comprend toutes les calculatrices de poche y compris les calculatrices programmables, alphanumériques ou à écran graphique à condition que leur fonctionnement soit autonome et qu'il ne soit pas fait usage d'imprimante. Thérèse Eveilleau. Boulier. Epreuves Junior. Idécimalité de nombres. Ensembles de nombres - webclasse.fr. Convertir Puissance, Chevaux. Socle commun. Document proposé par Carole SIGNARBIEUX et Muriel MUNIER Conseillères Pédagogiques de Circonscription Présentation de quelques documents élaborés au sein du groupe de travail départemental sur le Socle commun notamment dans le cadre de la commande : " travailler sur des tâches complexes pour évaluer les items du Socle commun.
" La tâche complexe fait partie intégrante de la notion de compétence, comme le rappelle le préambule du Socle commun " maîtriser le socle commun, c'est être capable de mobiliser ses acquis dans des tâches et des situations complexes, à l'école puis dans sa vie d'adulte […]" Fiche terminologie à télécharger Le Socle commun : La scolarité obligatoire doit au moins garantir à chaque élève les moyens nécessaires à l'acquisition d'un socle commun constitué d'un ensemble de connaissances et de compétences.
Taches complexes academiques. La tâche complexe Un groupe IREM - Rectorat de Clermont-Ferrand, crée des outils d’aide à l’élaboration de tâches complexes.

Composition de l’équipe : professeurs de collège, lycée et université. Les outils actuellement élaborés par l’équipe sont des documents de travailsusceptibles d'être modifiés et complétés.Chaque outil en ligne sur le portail académique comporte une fiche professeur, une fiche élève, Les dossiers - Le jeu du « franc carreau ».
- 12 janvier 2013 - David Nowacki [1]. et Hervé Milliard [2].

Le rapport de la commission de réflexion sur l’enseignement des mathématiques [3]. exprimait en ces termes un des enjeux de cet enseignement :« La notion de probabilité est abordée dès la classe de troisième à partir d’exemples concrets et de situations simples que l’élève peut se représenter sans aucune difficulté. C’est en observant et en relevant les résultats de nombreuses épreuves répétées que l’on pourra montrer la stabilisation des fréquences. » C’est pour illustrer ces directions que nous avons choisi de montrer divers aspects de l’un des thèmes d’étude proposés dans le document « Ressources pour la classe de seconde » Probabilités et Statistiques.
Cette activité peut être traitée, dans l’ordre : 1. Nous la traitons depuis une première approche pour les élèves de troisième jusqu’à des prolongements que l’on peut faire en classe de seconde, voire en première. Partie 0. Partie I (niveau collège). 1. 1. 1. 3. Questions Franc-Carreau. Multiplications. Décomposition. Problèmes de Maths. Les défis sont reliés à différents domaines des mathématiques et exigent l'application de stratégies diverses.

Ils sont tous résolus et partagés en trois séries. Les défis de la série B sont généralement de difficulté moindre que ceux de la série A (ci-après). Les défis de la série C exigent une meilleure connaissance des mathématiques. Choisissez les problèmes que vous désirez. nRécréomath vous présente plus de 7500 problèmes, énigmes et jeux. n Récréomath reçoit une moyenne de 2000 visiteurs par jour. n Visitez les 13 livres édités par Récréomath. nLisez les 26 articles publiés par Récréomath. n Si vous désirez faire une recherche dans Récréomath, allez dans Google, tapez récréomath et l'objet de votre recherche, au besoin entre guillemets. Franc carreau. Le théorème de Pythagore et Garfield. Le théorème de Pythagore, démontré par un Président des Etats-Unis Histoire -- Démonstrations classiques Géométrie -- Triangle On doit à Abraham Garfield (1831-1881) qui fut le vingtième Président des Etats-Unis, une démonstration du théorème de Pythagore, basée sur la figure suivante : L'aire du trapèze BCDE est : (a+b)×(a+b)/2=a2/2+b2/2+ab.
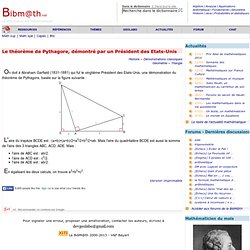
Mais l'aire du quadrilatère BCDE est aussi la somme de l'aire des 3 triangles ABC, ACD, ADE. Inégalité triangulaire. Bon, c'est dans le livre I dont la conclusion est le théorème de Pythagore ; il s'agit de la proposition 20 : Dans tout triangle, deux côtés pris ensemble de quelque façon que ce soit sont plus grand que le côté restant.
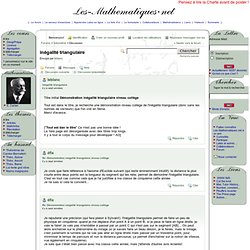
Voici la démonstration (traduction de Bernard Vitrac) ; je coupe les redondances classiques d'Euclide (le rituel euclidien). "Que soit conduite jusqu'au point , que soit placé " (bref, on construit sur la demi-droite d'origine et ne contenant pas tel que ; ceci repose sur la proposition 2 qui permet de reporter la longueur d'un segment sur une droite à partir d'un point ; à noter que cette proposition est de peu d'utilité, il suffit de tracer le cercle de centre passant par , mais Euclide ne répète jamais deux fois la même chose.) "Que soit jointe" (axiome mener une droite passant par deux points donnés) Tout repose donc sur cette proposition 19 qui est précédée de quelques lemmes.
Géométrie euclidienne élémentaire. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges A l'origine, la géométrie est la mesure de la Terre : en grec, gê = terre et metron = mesure.

En premier lieu, Euclide définit les objets usuels de la géométrie plane : point : ce dont la partie est nulle; ligne (finie) : longueur sans largeur dont les extrémités sont des points; droite : ligne qui est également (de manière égale) placée entre ses points; droites (distinctes) parallèles d'un même plan : droites qui, prolongées indéfiniment d'un côté ou de l'autre, ne se rencontrent pas.
Calculatrice graphique, scientifique et financière - Texas Instruments Gamme de calculatrices graphiques et scientifiques TI - France. CALCULATRICES CASIO : ENTREZ DANS UNE NOUVELLE ÈRE ! ActivInspire. Licence ActivInspire Personal Edition Produits tiers (non Promethean) Les utilisateurs sont autorisés à utiliser ActivInspire Personal Edition avec des produits tiers, à condition qu'ils aient préalablement demandé une licence Consentement de l'enseignant. La licence Consentement de l'enseignant est accordée exclusivement à des fins d'exploitation des ressources provenant de Promethean Planet sur du matériel tiers.
Toute utilisation du logiciel avec des produits tiers ne respectant pas les conditions énoncées ci-dessus constitue une violation de la licence ActivInspire Personal Edition et nécessite l'achat d'une licence ActivInspire Professional Edition. Demander maintenant Mises à niveau via un ActivHub La mise à niveau vers ActivInspire Professional Edition via un ActivHub est uniquement autorisée dans le cas où vous avez acheté des unités ActivExpression, ActiVote ou un ActivPanel et qu'ils sont connectés à l'ActivHub. Licences ActivInspire. Théorème de la médiane. Un article de Wikipédia, l'encyclopédie libre. Il existe plusieurs versions de ce théorème dont certaines font appel au produit scalaire. Enfin, il existe aussi une relation vectorielle liant les vecteurs portés par les côtés et celui porté par la médiane.
Activité de calcul de pi au collège. Tableau récapitulatif des tâches complexes - Préambule Toutes ces activités ont été choisies car elles développent des compétences transversales comme la prise d’initiative, l’autonomie et la démarche scientifique. — Sixième — Cinquième — Quatrième — Troisième — Seconde Sixième Le puzzle de Brousseau Cette activité est bien connue dans la didactique des Mathématiques. Elle n’a pas été conçue par un membre de notre groupe, mais nous tenions à la faire figurer dans ce tableau car elle permet, entre autre, de « casser » le modèle additif pour les agrandissements.
Retour au menu Cinquième La pêche à pieds Cette activité peut également être proposée en classe de 4e. Quatrième. Usages du TBI en maths. Quelles activités mener avec un TBI ? Des exemples en images : Voir une vidéo sur l'usage du tableau interactif en géométrie dans l'espace (SCEREN : Agence des usages) Des exemples d'usages variés, présentés lors d'une rencontre des utilisateurs de l'académie de Versailles (Février 2009) Les activités présentées se déroulent le plus souvent en classe entière. La lecture des compte-rendus de ces activités permet de mieux comprendre les apports du TBI (voir la rubrique Apports).
Maths et pb. Le numérique en Maths.