

Citizen Maths. Poincaré Conjecture - Numberphile. Courbe de Peano. Courbe de Peano. After 400 years, mathematicians find a new class of shapes. The works of the Greek polymath Plato have kept people busy for millennia.
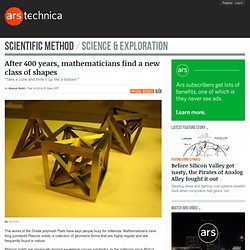
Mathematicians have long pondered Platonic solids, a collection of geometric forms that are highly regular and are frequently found in nature. Platonic solids are generically termed equilateral convex polyhedra. In the millennia since Plato's time, only two other collections of equilateral convex polyhedra have been found: Archimedean solids (including the truncated icosahedron) and Kepler solids (including rhombic polyhedra). Nearly 400 years after the last class was described, mathematicians claim that they may have now identified a new, fourth class, which they call Goldberg polyhedra.
Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses. Author Affiliations Edited by Patrick Fowler, The University of Sheffield, Sheffield, United Kingdom, and accepted by the Editorial Board January 7, 2014 (received for review June 10, 2013)

Wikipedia-size maths proof too big for humans to check - physics-math - 17 February 2014. If no human can check a proof of a theorem, does it really count as mathematics?
That's the intriguing question raised by the latest computer-assisted proof. It is as large as the entire content of Wikipedia, making it unlikely that will ever be checked by a human being. "It might be that somehow we have hit statements which are essentially non-human mathematics," says Alexei Lisitsa of the University of Liverpool, UK, who came up with the proof together with colleague Boris Konev. The proof is a significant step towards solving a long-standing puzzle known as the Erdős discrepancy problem. It was proposed in the 1930s by the Hungarian mathematician Paul Erdős, who offered $500 for its solution. [1402.2184] A SAT Attack on the Erdos Discrepancy Conjecture. Computers are providing solutions to math problems that we can't check. How to work out proofs in Analysis I. Now that we’ve had several results about sequences and series, it seems like a good time to step back a little and discuss how you should go about memorizing their proofs.

And the very first thing to say about that is that you should attempt to do this while making as little use of your memory as you possibly can. Suppose I were to ask you to memorize the sequence 5432187654321. Would you have to learn a string of 13 symbols? No, because after studying the sequence you would see that it is just counting down from 5 and then counting down from 8.
John Baez on the number 8. John Baez on the number 5. John Baez on the number 24. ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12. The Infinite Hotel Paradox - Jeff Dekofsky. The On-Line Encyclopedia of Integer Sequences® (OEIS®) Curly chaps. Euler spiral. A double-end Euler spiral.
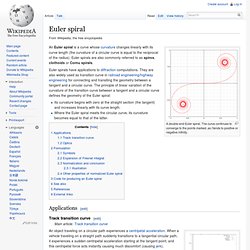
The curve continues to converge to the points marked, as t tends to positive or negative infinity. An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals. Probabilités et Statistique. Prime Spirals - Numberphile. Heady mathematics: Describing popping bubbles in a foam. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Reading Materials by Eugene Wigner "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," in Communications in Pure and Applied Mathematics, vol. 13, No.

I (February 1960). New York: John Wiley & Sons, Inc. Copyright © 1960 by John Wiley & Sons, Inc. Mathematics, rightly viewed, possesses not only truth, but supreme beautya beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.
THERE IS A story about two friends, who were classmates in high school, talking about their jobs. Naturally, we are inclined to smile about the simplicity of the classmate's approach. The preceding two stories illustrate the two main points which are the subjects of the present discourse. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Reading Materials by R.

W. HAMMING Reprinted From: The American Mathematical Monthly Volume 87 Number 2 February 1980. Is Math a Feature of the Universe or a Feature of Human Creation? Biggest Thing in the Universe - Sixty Symbols. Dragon Curve - Numberphile. New Largest Known Prime Number - Numberphile. After almost 20 years, math problem falls. Mathematicians and engineers are often concerned with finding the minimum value of a particular mathematical function.
That minimum could represent the optimal trade-off between competing criteria — between the surface area, weight and wind resistance of a car’s body design, for instance. In control theory, a minimum might represent a stable state of an electromechanical system, like an airplane in flight or a bipedal robot trying to keep itself balanced. There, the goal of a control algorithm might be to continuously steer the system back toward the minimum. For complex functions, finding global minima can be very hard. But it’s a lot easier if you know in advance that the function is convex, meaning that the graph of the function slopes everywhere toward the minimum. Almost 20 years later, researchers in MIT’s Laboratory for Information and Decision Systems have finally answered that question.
Random Numbers - Numberphile. Encryption and HUGE numbers - Numberphile. Who was the REAL Good Will Hunting? - Numberphile. The problem in Good Will Hunting - Numberphile. Squaring the Circle - Numberphile. 5 and Penrose Tiling - Numberphile. Un nouveau nombre premier à 17 millions de chiffres. Unicity distance. Consider an attack on the ciphertext string "WNAIW" encrypted using a Vigenère cipher with a five letter key.
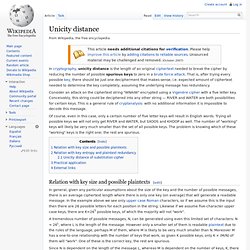
Conceivably, this string could be deciphered into any other string — RIVER and WATER are both possibilities for certain keys. This is a general rule of cryptanalysis: with no additional information it is impossible to decode this message. Of course, even in this case, only a certain number of five letter keys will result in English words.
Trying all possible keys we will not only get RIVER and WATER, but SXOOS and KHDOP as well. The number of "working" keys will likely be very much smaller than the set of all possible keys. Relation with key size and possible plaintexts[edit] In general, given any particular assumptions about the size of the key and the number of possible messages, there is an average ciphertext length where there is only one key (on average) that will generate a readable message. How to theoretically turn a sphere inside out. Abc Conjecture - Numberphile. IDTIMWYTIM: Stochasticity - THAT'S Random. Polymathematics. Proof claimed for deep connection between primes.
The usually quiet world of mathematics is abuzz with a claim that one of the most important problems in number theory has been solved.

Mathematician Shinichi Mochizuki of Kyoto University in Japan has released a 500-page proof of the abc conjecture, which proposes a relationship between whole numbers — a 'Diophantine' problem. The abc conjecture, proposed independently by David Masser and Joseph Oesterle in 1985, might not be as familiar to the wider world as Fermat’s Last Theorem, but in some ways it is more significant.
“The abc conjecture, if proved true, at one stroke solves many famous Diophantine problems, including Fermat's Last Theorem,” says Dorian Goldfeld, a mathematician at Columbia University in New York. Infinity is bigger than you think - Numberphile. Root 2 - Numberphile. 1 and Prime Numbers - Numberphile. 998,001 and its Mysterious Recurring Decimals - Numberphile. 6,000,000 and Abel Prize - Numberphile. Mathgen paper accepted! I’m pleased to announce that Mathgen has had its first randomly-generated paper accepted by a reputable journal!
On August 3, 2012, a certain Professor Marcie Rathke of the University of Southern North Dakota at Hoople submitted a very interesting article to Advances in Pure Mathematics, one of the many fine journals put out by Scientific Research Publishing. Tel.archives-ouvertes.fr/docs/00/42/28/54/ANNEX/Slides_phd.pdf. Mdpdanech.free.fr/theses/these_freville.pdf. Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance. Social Science Research Network (SSRN) Home Page. Numberphile - Videos about Numbers and Stuff. Les rhinos sauvés par les maths? « Sachant que le nombre de rhinocéros en liberté en Afrique du Sud avoisine les 20 000, que l’augmentation du braconnage suit une courbe exponentielle et que le prix de la corne atteint au marché noir 50 000 euros le kilo, vous répondrez à la question suivante : l'élevage intensif de rhinocéros dans des fermes et l'ouverture officielle d'un marché de la corne permettraient-ils: 1) de faire suffisamment chuter les prix pour décourager le braconnage, 2) de générer assez d'argent pour protéger et gérer les représentants de l’espèce en liberté dans les parcs nationaux?
Vous tiendrez compte, dans vos projections du coût des mesures de protection et de lutte contre le braconnage ». Un MISG est un atelier de plusieurs jours, durant lequel chercheurs universitaires et étudiants travaillent en collaboration avec des représentants de l'industrie sur des problèmes de recherche appliquée à la réalité locale. L’exercice, pour le moment, n’en reste pas moins théorique. Base 12 - Numberphile. Tau vs Pi Smackdown - Numberphile. Julia set. A Julia set Three-dimensional slices through the (four-dimensional) Julia set of a function on the quaternions. The Julia set of a function f is commonly denoted J(f), and the Fatou set is denoted F(f).[1] These sets are named after the French mathematicians Gaston Julia[2] and Pierre Fatou[3] whose work began the study of complex dynamics during the early 20th century.
Formal definition[edit] Problems with Zero - Numberphile. 1,296 and Yahtzee - Numberphile. The Most Mathematical Flag - Numberphile. Arxiv.org/pdf/math.NT/0404188.pdf. Statistique multivariée. Un article de Wikipédia, l'encyclopédie libre. Catalog Page for PIA16075. This composite image, with magnified insets, depicts the first laser test by the Chemistry and Camera, or ChemCam, instrument aboard NASA's Curiosity Mars rover.
The composite incorporates a Navigation Camera image taken prior to the test, with insets taken by the camera in ChemCam. The circular insert highlights the rock before the laser test. The square inset is further magnified and processed to show the difference between images taken before and after the laser interrogation of the rock. The test took place on Aug. 19, 2012. In the composite, the fist-sized rock, called "Coronation," is highlighted. The widest context view in this composite comes from Curiosity's Navigation Camera. Intro to Cryptography. Le réseau complexe du jeu de go. 04/05 > BE Allemagne 566 > Les mathématiques pour optimiser le marché des énergies renouvelables.
EnergieLes mathématiques pour optimiser le marché des énergies renouvelables Les gestionnaires des réseaux de distribution sont par définition responsables de la fourniture d'électricité. Jean-Baptiste Michel: The mathematics of history. Un monde de fractales dans un fichier de 4 kilobytes. De l’inexactitude dans nos ordinateurs. S’il y a bien un endroit où l’on peut être certain des informations que l’on traite, c’est dans les puces de nos ordinateurs. L'intelligence collective au service des décideurs. High School Mathematics Extensions/Discrete Probability. Introduction[edit] Probability theory is one of the most widely applicable mathematical theories. It deals with uncertainty and teaches you how to manage it. It is simply one of the most useful theories you will ever learn.
Ulam spiral. Ulam spiral of size 200×200. Black dots represent prime numbers. Diagonal, vertical, and horizontal lines with a high density of prime numbers are clearly visible. The Ulam spiral, or prime spiral (in other languages also called the Ulam Cloth) is a simple method of visualizing the prime numbers that reveals the apparent tendency of certain quadratic polynomials to generate unusually large numbers of primes. It was discovered by the mathematician Stanislaw Ulam in 1963, while he was doodling during the presentation of a "long and very boring paper" at a scientific meeting. Shortly afterwards, in an early application of computer graphics, Ulam with collaborators Myron Stein and Mark Wells used MANIAC II at Los Alamos Scientific Laboratory to produce pictures of the spiral for numbers up to 65,000.
In an addendum to the Scientific American column, Gardner mentions work of the herpetologist Laurence M. Doodling in Math: Sick Number Games. Proof of the existence of God set down on paper.
Jeunes et minces? Les maths contre la retouche photo. Des chercheurs du Dartmouth College ont mis au point un algorithme capable de déterminer quand une photo a été retouchée hors de proportion par des outils comme Photoshop, un procédé abondamment utilisé dans les photos de mode et dans les magazines de célébrités et dénoncé par les spécialistes en santé publique. Le logiciel mis au point par Hani Farid, décrit dans une publication dans les Proceedings of the National Academy of Sciences, permettrait de quantifier la retouche effectuée sur une photo, et donc de déterminer objectivement à partir de quand on exagère.
Empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf. Logic. Game Theory. Cryptographie. Un article de Wikipédia, l'encyclopédie libre. Cypherpunk. Un article de Wikipédia, l'encyclopédie libre. How Bull Markets Evolve into Bubbles. Graphe planaire. Théorème des quatre couleurs. Problème NP-complet. Mba.tuck.dartmouth.edu/pages/faculty/andrew.bernard/oscars.pdf. De l’esthétique des fractions continues. Votre boulanger est-il discret? (1/2) Boulanger: la saga continue (2/2)
Topology - Geometry. Logic. Chaos theory. Hasse diagram. Sabermetrics. Benford's law.