

Personal and Historical Perspectives of Hans Bethe. Pandigital Approximations. The digits 1-9 can work some impressive tricks: The first formula, found by B.
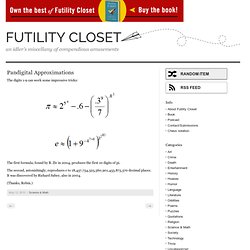
Ziv in 2004, produces the first 10 digits of pi. The second, astonishingly, reproduces e to 18,457,734,525,360,901,453,873,570 decimal places. It was discovered by Richard Sabey, also in 2004. (Thanks, Robin.) Courses & Video Lectures. Fractals. LiveMath™ Software Products. An Intuitive Explanation of Fourier Theory.
Steven Lehar slehar@cns.bu.edu Fourier theory is pretty complicated mathematically. But there are some beautifully simple holistic concepts behind Fourier theory which are relatively easy to explain intuitively. There are other sites on the web that can give you the mathematical formulation of the Fourier transform. I will present only the basic intuitive insights here, as applied to spatial imagery. Basic Principles: How space is represented by frequency Higher Harmonics: "Ringing" effects An Analog Analogy: The Optical Fourier Transform Fourier Filtering: Image Processing using Fourier Transforms Basic Principles Fourier theory states that any signal, in our case visual images, can be expressed as a sum of a series of sinusoids. These three values capture all of the information in the sinusoidal image. The magnitude of the sinusoid corresponds to its contrast, or the difference between the darkest and brightest peaks of the image.
Back to top Higher Harmonics and "Ringing" effects. Fast and usable calculator. Octave. GNU Octave is a high-level interpreted language, primarily intended for numerical computations.

It provides capabilities for the numerical solution of linear and nonlinear problems, and for performing other numerical experiments. It also provides extensive graphics capabilities for data visualization and manipulation. Octave is normally used through its interactive command line interface, but it can also be used to write non-interactive programs. The Octave language is quite similar to Matlab so that most programs are easily portable. Octave is distributed under the terms of the GNU General Public License. Version 4.0.0 has been released and is now available for download. An official Windows binary installer is also available from A list of important user-visible changes is availble at by selecting the Release Notes item in the News menu of the GUI, or by typing news at the Octave command prompt.
Thanks to the many people who contributed to this release! Sin & Cos: The Programmer's Pals! 9 Mental Math Tricks. Math can be terrifying for many people.

This list will hopefully improve your general knowledge of mathematical tricks and your speed when you need to do math in your head. 1. Multiplying by 9, or 99, or 999 Multiplying by 9 is really multiplying by 10-1. So, 9×9 is just 9x(10-1) which is 9×10-9 which is 90-9 or 81. Let’s try a harder example: 46×9 = 46×10-46 = 460-46 = 414. One more example: 68×9 = 680-68 = 612. To multiply by 99, you multiply by 100-1. So, 46×99 = 46x(100-1) = 4600-46 = 4554. Impress your friends with mental Math tricks » Fun Math Blog. See Math tricks on video at the Wild About Math!

Mathcasts page. Being able to perform arithmetic quickly and mentally can greatly boost your self-esteem, especially if you don't consider yourself to be very good at Math. And, getting comfortable with arithmetic might just motivate you to dive deeper into other things mathematical. This article presents nine ideas that will hopefully get you to look at arithmetic as a game, one in which you can see patterns among numbers and pick then apply the right trick to quickly doing the calculation.
Uncoiling the spiral: Maths and hallucinations. December 2009 You can read a more accessible version of this article here.
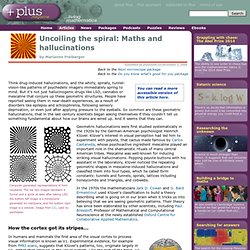
Think drug-induced hallucinations, and the whirly, spirally, tunnel-vision-like patterns of psychedelic imagery immediately spring to mind. But it's not just hallucinogenic drugs like LSD, cannabis or mescaline that conjure up these geometric structures. People have reported seeing them in near-death experiences, as a result of disorders like epilepsy and schizophrenia, following sensory deprivation, or even just after applying pressure to the eyeballs. So common are these geometric hallucinations, that in the last century scientists began asking themselves if they couldn't tell us something fundamental about how our brains are wired up. Computer generated representations of form constants. Science Mysteries, Fibonacci Numbers and Golden section in Nature. Golden Ratio & Golden Section : : Golden Rectangle : : Golden Spiral Golden Ratio & Golden Section In mathematics and the arts, two quantities are in the golden ratio if the ratio between the sum of those quantities and the larger one is the same as the ratio between the larger one and the smaller.
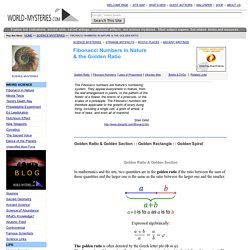
Expressed algebraically: The golden ratio is often denoted by the Greek letter phi (Φ or φ). The figure of a golden section illustrates the geometric relationship that defines this constant.