

1976_rockafellar_monotone_operators_proximal_point_algorithm.
Hyper-Textbook: Optimization Models and Applications. Optimization in Robotics, Machine Learning, and Control, Part II. CSE 711: Convex Optimization in Robotics, Machine Learning, and Control, Part I (Fall 2012 Seminar) Lectures on Linear Programming: Foundations and Extensions Graduate level. Non-linear programming. Interesting applications. Opti in finance. Books. Matrix Analysis Courses. Maryam Fazel. I am an Assistant Professor in EE, and have Adjunct appointments in CSE, Math, and Statistics.

My research interests lie in the intersection of mathematical optimization, data analysis, and control theory. Prior to joining UW EE, I was a Research Scientist at the Control and Dynamical Systems Department at Caltech. I received my PhD in Electrical Engineering from Stanford University where I was part of the Information Systems Lab. In 2009, I received an NSF Career Award and the UW EE Outstanding Teaching Award. My entry in the Mathematics Genealogy Project. News and Events West Coast Optimization Meeting (WCOM), May 2-3, 2014 on UW campus. Research Interests Convex Optimization; Parsimonious Modeling and Compressed Sensing; Matrix Rank Minimization; Distributed Online Optimization; Applications in large-scale data analysis and machine learning, signal processing, and system identification.
Research group Students: WIKIMIZATION - Wikimization. INTELLIGENT-OPTIMIZATION.ORG.
Sudoku problem. Guestrin's Optimization Course. Class lectures: Mondays and Wednesdays 10:30-11:50am in GHC 4307 Recitations: Thursdays 5:00 - 6:20, Hammerschlag Hall B103 Essentially, every problem in computer science and engineering can be formulated as the optimization of some function under some set of constraints.

This universal reduction automatically suggests that such optimization tasks are intractable. Fortunately, most real world problems have special structure, such as convexity, locality, decomposability or submodularity. These properties allow us to formulate optimization problems that can often be solved efficiently. Students entering the class should have a pre-existing working knowledge of algorithms, though the class has been designed to allow students with a strong numerate background to catch up and fully participate. Announcement Emails Class announcements will be broadcasted using a group email list: Please subscribe to the 10725-announce list page.
Discussion Group Textbooks Grading Auditing Homework policy. 8.4.2 Optimal Solution for TSP using Branch and Bound. Suppose it is required to minimize an objective function.

Suppose that we have a method for getting a lower bound on the cost of any solution among those in the set of solutions represented by some subset. If the best solution found so far costs less than the lower bound for this subset, we need not explore this subset at all. Let S be some subset of solutions. Let Suppose we want a lower bound on the cost of a subset of tours defined by some node in the search tree. In the above solution tree, each node represents tours defined by a set of edges that must be in the tour and a set of edges that may not be in the tour. These constraints alter our choices for the two lowest cost edges at each node. Symmetric TSP's based on US geography.
Global Optimization Software. Global Search, As Timely As Ever ``Consider everything.

Keep the good. Avoid evil whenever you notice it.''(1 Thess. 5:21-22) This file is part of my global optimization web site. Public Domain Systems. INTELLIGENT-OPTIMIZATION.ORG. Www.me.utexas.edu/~jensen/ORMM/supplements/units/ip_methods/other_bb.pdf. Gram–Schmidt process. The first two steps of the Gram–Schmidt process The method is named after Jørgen Pedersen Gram and Erhard Schmidt but it appeared earlier in the work of Laplace and Cauchy.
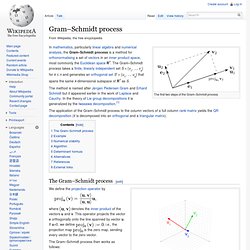
In the theory of Lie group decompositions it is generalized by the Iwasawa decomposition.[1] The Gram–Schmidt process[edit] The Gram-Schmidt process being executed on three linearly independent, non-orthogonal vectors of a basis for R3. Click on image for details. where denotes the inner product of the vectors u and v. . i.e., the projection map is the zero map, sending every vector to the zero vector. The Gram–Schmidt process then works as follows: The sequence u1, ..., uk is the required system of orthogonal vectors, and the normalized vectors e1, ..., ek form an orthonormal set.
To check that these formulas yield an orthogonal sequence, first compute ‹ u1,u2 › by substituting the above formula for u2: we get zero. The Gram–Schmidt process also applies to a linearly independent countably infinite sequence {vi}i. With.