

Géométrie algébrique. Un article de Wikipédia, l'encyclopédie libre.
La géométrie algébrique est un domaine des mathématiques qui, historiquement, s'est d'abord intéressé à des objets géométriques (courbes, surfaces...) dont les coordonnées vérifiaient des équations ne faisant intervenir que des sommes et des produits (par exemple le cercle unité dans le plan rapporté à un repère orthonormé admet pour équation ). La simplicité de cette définition fait qu'elle embrasse un grand nombre d'objets et qu'elle permet de développer une théorie riche. Les besoins théoriques ont contraint les mathématiciens à introduire des objets plus généraux dont l'étude a eu des applications bien au-delà de la simple géométrie algébrique ; en théorie des nombres par exemple, cela a conduit à une preuve du grand théorème de Fermat.
Cette branche des mathématiques n'a désormais plus grand-chose à voir avec la géométrie analytique dont elle est en partie issue. Histoire[modifier | modifier le code] . S'annule donc sur l'axe . Où . . . Nuclear space. In mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces.
The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size. Vector spaces whose elements are "smooth" in some sense tend to be nuclear spaces; a typical example of a nuclear space is the set of smooth functions on a compact manifold. All finite-dimensional vector spaces are nuclear (because every operator on a finite-dimensional vector space is nuclear).
There are no Banach spaces that are nuclear, except for the finite-dimensional ones. In practice a sort of converse to this is often true: if a "naturally occurring" topological vector space is not a Banach space, then there is a good chance that it is nuclear. Although important,[citation needed] nuclear spaces are not explicitly used in practice. Much of the theory of nuclear spaces was developed by Alexander Grothendieck and published in (Grothendieck 1955). and. Rappels mathématiques, compléments d'électrostatique et magnétostatique - Rappels sur les coordonnées polaires, sphériques et cylindriques.
Le paragraphe précédent nous montre que dans le cas du cercle, il peut être avantageux de travailler dans d'autres systèmes de coordonnées que les cartésiennes orthonormées directes traditionnelles.
En fait, nous verrons que les coordonnées cartésiennes servent surtout en physique à traiter les cas généraux, les cas mono-dimensionnels, ou à établir des relations, mais souvent les problèmes étudiés présentent des symétries telles qu'il vaudra mieux se placer en coordonnées de type polaire. À deux dimensions on repère un point par sa distance à l'origine et par l'angle que fait le vecteur avec le vecteur d'une base cartésienne de référence. Métrique riemannienne. Un article de Wikipédia, l'encyclopédie libre.
En géométrie différentielle, les métriques riemanniennes sont la notion de base de la géométrie riemannienne. La première introduction a été donnée par Bernhard Riemann en 1854. Cependant, son article sur le sujet a été publié après sa mort, en 1868. La même année, Hermann von Helmholtz publie des résultats analogues. Les métriques riemanniennes sont des familles différentiables de formes quadratiques définies positives. Définitions[modifier | modifier le code] Sur un fibré vectoriel E→M, une métrique riemannienne g est la donnée d'un produit scalaire gx sur chaque fibre Ex qui dépende de manière lisse du point de base x variant dans M. Pour deux fibrés riemanniens (E,g) et (F,g' ) sur M, un morphisme de fibrés riemanniens f:(E,g)→(E,g' ) est un morphisme de fibrés vectoriels f:E→E' tel que, pour tout point x de M, l'application linéaire fx:Ex→Fx est une isométrie linéaire, c'est-à-dire :
Espace de Minkowski. Un article de Wikipédia, l'encyclopédie libre.
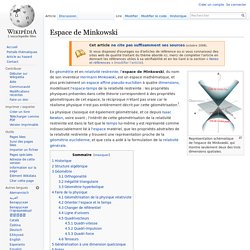
Représentation schématique de l'espace de Minkowski, qui montre seulement deux des trois dimensions spatiales. En géométrie et en relativité restreinte, l’espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace mathématique, et plus précisément un espace affine pseudo-euclidien à quatre dimensions, modélisant l'espace-temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie correspondent à des propriétés géométriques de cet espace, la réciproque n'étant pas vraie car le réalisme physique n'est pas entièrement décrit par cette géométrisation[1]. Historique[modifier | modifier le code] Structure algébrique[modifier | modifier le code] L'espace de Minkowski étant un espace affine de dimension quatre, il correspond à la donnée d'un point O (l'origine du repère) et d'un espace vectoriel (dit associé) de dimension quatre (sur ou telle que [3], où.
Alexandre Grothendieck. Un article de Wikipédia, l'encyclopédie libre.
Alexandre Grothendieck Alexandre Grothendieck en 1970. Il est considéré comme le refondateur de la géométrie algébrique et, à ce titre, comme l'un des plus grands mathématiciens du XXe siècle[4]. Il était connu pour son intuition extraordinaire et sa capacité de travail exceptionnelle. La médaille Fields lui a été décernée en 1966. Biographie[modifier | modifier le code] Ascendance et enfance[modifier | modifier le code] Sacha Schapiro, son père. Sacha Schapiro, son père[5], également connu sous le nom de Tanaroff, est un anarchiste militant ukrainien né à Novozybkov, ville située aujourd’hui en Russie, dans l'oblast de Briansk.