

Coursera.org. Self Publishing - Lulu.com. 12 Dozen Places To Educate Yourself Online For Free. Atomic orbital. The shapes of the first five atomic orbitals: 1s, 2s, 2px, 2py, and 2pz.
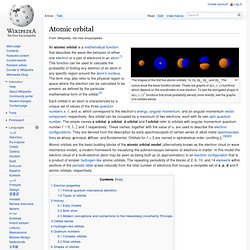
The colors show the wave function phase. These are graphs of ψ(x, y, z) functions which depend on the coordinates of one electron. To see the elongated shape of ψ(x, y, z)2 functions that show probability density more directly, see the graphs of d-orbitals below. Each orbital in an atom is characterized by a unique set of values of the three quantum numbers n, ℓ, and m, which correspond to the electron's energy, angular momentum, and an angular momentum vector component, respectively.
Any orbital can be occupied by a maximum of two electrons, each with its own spin quantum number. Atomic orbitals are the basic building blocks of the atomic orbital model (alternatively known as the electron cloud or wave mechanics model), a modern framework for visualizing the submicroscopic behavior of electrons in matter. Electron properties[edit] Wave-like properties: Particle-like properties: Types of orbitals[edit] History[edit] Background: Atoms and Light Energy. Inside the Atom Just like bricks are the building blocks of a home, atoms are the building blocks of matter.
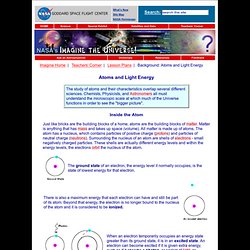
Matter is anything that has mass and takes up space (volume). All matter is made up of atoms. The atom has a nucleus, which contains particles of positive charge (protons) and particles of neutral charge (neutrons). Surrounding the nucleus of an atom are shells of electrons - small negatively charged particles. Light Energy Each orbital has a specific energy associated with it. The illustrations on this page are simplified versions of real atoms, of course. Identifying Individual Types of Atoms Transitions among the various orbitals are unique for each element because the energy levels are uniquely determined by the protons and neutrons in the nucleus.
Open Yale courses. Security Now! Episode Archive. OpenClassroom. Full courses.

Short Videos. Free for everyone. Learn the fundamentals of human-computer interaction and design thinking, with an emphasis on mobile web applications. A practical introduction to Unix and command line utilities with a focus on Linux. Introduction to fundamental techniques for designing and analyzing algorithms, including asymptotic analysis; divide-and-conquer algorithms and recurrences; greedy algorithms; data structures; dynamic programming; graph algorithms; and randomized algorithms. Database design and the use of database management systems (DBMS) for applications.
Machine learning algorithms that learn feature representations from unlabeled data, including sparse coding, autoencoders, RBMs, DBNs. Introduction to discrete probability, including probability mass functions, and standard distributions such as the Bernoulli, Binomial, Poisson distributions. Academic Video Lectures. Khan Academy. Free Online Course Materials.