

Bilinear Mpping. Section1-4a-new.pdf. Linear Transformation - OpenSeesWiki. From OpenSeesWiki This command is used to construct a linear coordinate transformation (LinearCrdTransf) object, which performs a linear geometric transformation of beam stiffness and resisting force from the basic system to the global-coordinate system.
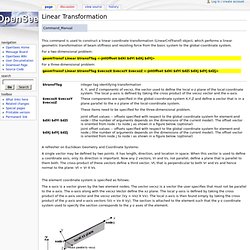
For a two-dimensional problem: For a three-dimensional problem: A refresher on Euclidean Geometry and Coordinate Systems: A single vector may be defined by two points. The element coordinate system is specified as follows: The x-axis is a vector given by the two element nodes; The vector vecxz is a vector the user specifies that must not be parallel to the x-axis. NOTE: When in 2D, local x and y axes are in the X-Y plane, where X and Y are global axes. Element 1 : tag 1 : vecxZ = zaxis. Linear Algebra/Linear Transformations. A linear transformation is an important concept in mathematics because many real world phenomena can be approximated by linear models.
Unlike a linear function, a linear transformation works on vectors as well as numbers. Motivations and definitions[edit] Say we have the vector in , and we rotate it through 90 degrees, to obtain the vector. Linear transformation in rotating electrical machines. Transformation of three phase electrical quantities to two phase quantities is a usual practice to simplify analysis of three phase electrical circuits.
Polyphase a.c machines can be represented by an equivalent two phase model provided the rotating polyphases winding in rotor and the stationary polyphase windings in stator can be expressed in a fictitious two axes coils. Transformation (function) Let us have a clear visualization of this. In day-to-day life we use computers in all fields. Let us consider this window. This window if maximized to full dimensions of the screen is the reference plane. Imagine one of the corners as the reference point or origin (0, 0). Consider a point P(x, y) in the corresponding plane.
X = x − h or x = X + h or h = x − X and Y = y − k or y = Y + k or k = y − Y. Replacing these values or using these equations in the respective equation we obtain the transformed equation or new reference axes, old reference axes, point lying on the plane. Linear canonical transformation. In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms.
It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). The LCT generalizes the Fourier, fractional Fourier, Laplace, Gauss–Weierstrass, Bargmann and the Fresnel transforms as particular cases. The name "linear canonical transformation" is from canonical transformation, a map that preserves the symplectic structure, as SL2(R) can also be interpreted as the symplectic group Sp2, and thus LCTs are the linear maps of the time–frequency domain which preserve the symplectic form. Definition[edit] The LCT can be represented in several ways; most easily,[1] it can be parameterized by a 2×2 matrix with determinant 1, i.e., an element of the special linear group SL2(R). To is defined as Special cases[edit] Composition[edit] then. Linear transform model (MRI) The linear transform model refers to a fundamental assumption guiding the analysis of functional Magnetic Resonance Imaging (fMRI) studies.
Specifically, the model holds that the fMRI signal is approximately proportional to a measure of local neural activity, averaged over a spatial extent of several millimeters and over a time period of several seconds. The linear transform model is a common and widespread assumption used in the interpretation of fMRI studies. However, some scientists suggest reasons exist to remain sceptical. Heeger and Ress, in a review of fMRI and its relation to neuronal activity, argue that it is a reasonable and useful approximation for local neural activity "for some recording sites, in some brain areas, using certain experimental protocols", but it is not under other circumstances.[1] Functional magnetic resonance imaging.
Semilinear transformation. Affine transformation. An image of a fern-like fractal that exhibits affine self-similarity.
Each of the leaves of the fern are related to each another leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. If and are affine spaces, then every affine transformation. Direct linear transformation. Direct linear transformation (DLT) is an algorithm which solves a set of variables from a set of similarity relations: for where and are known vectors, denotes equality up to an unknown scalar multiplication, and.
Transformation matrix. Is a column vector with n entries, then for some m×n matrix A, called the transformation matrix of T. There is an alternative expression of transformation matrices involving row vectors that is preferred by some authors. Uses[edit] Matrices allow arbitrary linear transformations to be represented in a consistent format, suitable for computation.[1] This also allows transformations to be concatenated easily (by multiplying their matrices). Put differently, a passive transformation refers to observation of the same event from two different coordinate frames.
Continuous linear functional. Linear map, wikipedia. Linear algebra.