

MA304 video (link) Basic Log Rules / Expanding Log Expressions. Basic Log Rules / Expanding Logarithmic Expressions (page 1 of 5) Sections: Basic log rules, Expanding, Simplifying, Trick questions, Change-of-Base formula You have learned various rules for manipulating and simplifying expressions with exponents, such as the rule that says that x3 × x5 equals x8 because you can add the exponents.
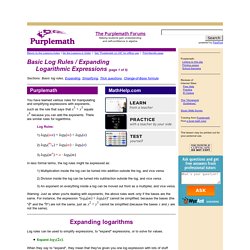
There are similar rules for logarithms. Log Rules: 1) logb(mn) = logb(m) + logb(n) 2) logb(m/n) = logb(m) – logb(n) 3) logb(mn) = n · logb(m) In less formal terms, the log rules might be expressed as: 1) Multiplication inside the log can be turned into addition outside the log, and vice versa. 2) Division inside the log can be turned into subtraction outside the log, and vice versa. 3) An exponent on everything inside a log can be moved out front as a multiplier, and vice versa. Warning: Just as when you're dealing with exponents, the above rules work only if the bases are the same. Expanding logarithms Expand log3(2x). I have a "2x" inside the log. Algebra - Exponential Functions. Algebra (Notes) / Exponential and Logarithm Functions / Exponential Functions[Notes][Practice Problems][Assignment Problems] Algebra - Notes Let’s start off this section with the definition of an exponential function.
Notice that the x is now in the exponent and the base is a fixed number. This is exactly the opposite from what we’ve seen to this point. To this point the base has been the variable, x in most cases, and the exponent was a fixed number. Before we get too far into this section we should address the restrictions on b. And these are constant functions and won’t have many of the same properties that general exponential functions have. Next, we avoid negative numbers so that we don’t get any complex values out of the function evaluation.
The function would be, and as you can see there are some function evaluations that will give complex numbers. Now, let’s take a look at a couple of graphs. Note as well that we could have written in the following way, Properties of where . And . Or. Logarithmic and exponential functions - Topics in precalculus. Exponential functions Inverse relations Exponential and logarithmic equations Creating one logarithm from a sum THE LOGARITHMIC FUNCTION WITH BASE b is the function y = logb x. b is normally a number greater than 1 (although it need only be greater than 0 and not equal to 1).
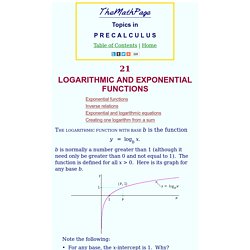
Note the following: • For any base, the x-intercept is 1. To see the answer, pass your mouse over the colored area. The logarithm of 1 is 0. y = logb1 = 0. • The graph passes through the point (b, 1). The logarithm of the base is 1. logbb = 1. Proper fractions. • The range of the function is all real numbers. • The negative y-axis is a vertical asymptote (Topic 18). Example 1. And here is the graph of y = ln (x − 2) -- which is its translation 2 units to the right. The x-intercept has moved from 1 to 3. Problem 1. This is a translation 3 units to the left. By definition: logby = x means bx = y. Corresponding to every logarithm function with base b, we see that there is an exponential function with base b: y = bx. Problem 2. Working with Exponents and Logarithms. What is an Exponent?

What is a Logarithm? A Logarithm goes the other way. It asks the question "what exponent produced this? ": And answers it like this: In that example: The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8) The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication) A Logarithm says how many of one number to multiply to get another number So a logarithm actually gives you the exponent as its answer: (Also see how Exponents, Roots and Logarithms are related.) Working Together Exponents and Logarithms work well together because they "undo" each other (so long as the base "a" is the same): They are "Inverse Functions" Doing one, then the other, gets you back to where you started: Doing ax then loga gives you x back again: Doing loga then ax gives you x back again: It is too bad they are written so differently ... it makes things look strange.
Going up, then down, returns you back again:down(up(x)) = x.