

B/ Le nombre d'or présent sur l'anatomie humaine - TPE : nombre d'or. Basé sur les dimensions du corps humain, un système de cinq mesures a été inventé : le quine.

Selon les époques, les mesures de bases étaient différentes mais la progression était semblable. Paume = 34 lignes Ligne : 1 grain d'orge Palme = 55 lignes Pouce : 12 lignes Empan = 89 lignes Pied : 12 pouces Pied = 144 lignes Toise : 6 pieds Coudée = 233 lignes On retrouve ici les nombres de la suite de Fibonacci ! Les partages du quine forment une suite additive, chaque dimension est la somme des deux précédentes, comme dans la suite de Fibonacci. Le rapport entre deux mesures consécutives est le nombre d'or, la suite peut en effet s'inscrire dans le pentagone. 1. 2. . - la 1ere phalange / la 2eme - la 2eme phalange / la 3eme 3. La tête de l'Homme s'inscrit dans des rectangle d'or : 4. . - la largeur totale des deux incisives centrales / leur hauteur (en bleu sur la photo) - la largeur de l'incisive centrale (celle de gauche ou celle de droite) / la largeur de la dent d'à côté (en orange sur la photo)
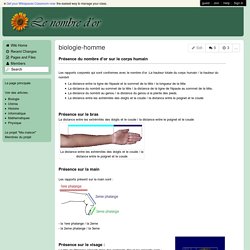
Le Nombre d'Or - biologie-homme. Présence du nombre d’or sur le corps humain Les rapports corporels qui sont conformes avec le nombre d’or :La hauteur totale du corps humain / la hauteur du nombrilLa distance entre la ligne de l'épaule et le sommet de la tête / la longueur de la têteLa distance du nombril au sommet de la tête / la distance de la ligne de l'épaule au sommet de la tête,La distance du nombril au genou / la distance du genou à la plante des pieds.La distance entre les extrémités des doigts et le coude / la distance entre le poignet et le coude Présence sur le bras La distance entre les extrémités des doigts et le coude / la distance entre le poignet et le coude Présence sur la main Les rapports présent sur la main sont :
Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . Il utilise également la racine carrée de 5 comme rapport. IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d'or.
Phyllotaxis. Pentagram & the Golden Ratio. The 'ratio' has become known as the golden ratio or golden section. This ratio can be found in many places: in art, architecture, and mathematics. The golden ratio also appears in comparing consecutive elements of certain kinds of sequences, most notably, the Fibonacci sequence, but other sequences also. For instance, take two numbers at random, say 2 and 6. Add them to get 8. Add 6 and 8 to get 14. You can find many rectangles in an icosahedron whose sides are in the golden ratio.Here's one. The Golden Rectangle can be subdivided into squares and additional smaller Golden Rectangles, again a process that seemingly could go on indefinitely.
What are the dimensions of square #3? 0.61803... : 1.00 :: 1.00 : 1.61803... or 0.61803... is to 1.00 as 1.00 is to 1.61803... or Ø - 1 : 1 :: 1 : Ø ® Ø2 - Ø = 1 Pictured here are what might be called a couple of "golden parallelograms", can you explain why that might be? Pictured below are some other "golden figures".