

Wallpaper group. Wallpaper groups are two-dimensional symmetry groups, intermediate in complexity between the simpler frieze groups and the three-dimensional crystallographic groups (also called space groups).
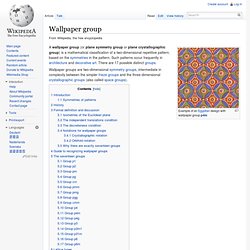
Introduction[edit] Wallpaper groups categorize patterns by their symmetries. Subtle differences may place similar patterns in different groups, while patterns that are very different in style, color, scale or orientation may belong to the same group. Consider the following examples: Examples A and B have the same wallpaper group; it is called p4m in the IUC notation and *442 in the orbifold notation. A complete list of all seventeen possible wallpaper groups can be found below. List of aperiodic sets of tiles. In geometry, a tiling is a partition of the plane (or any other geometric setting) into closed sets (called tiles), without gaps or overlaps (other than the boundaries of the tiles).[1] A tiling is considered periodic if there exist translations in two independent directions which map the tiling onto itself.
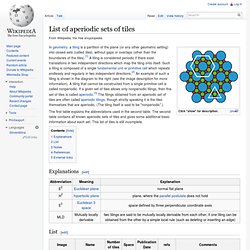
Such a tiling is composed of a single fundamental unit or primitive cell which repeats endlessly and regularly in two independent directions.[2] An example of such a tiling is shown in the diagram to the right (see the image description for more information). A tiling that cannot be constructed from a single primitive cell is called nonperiodic. Pentomino. Comparison of pentomino labeling schemes.

The first naming convention is the one used in this article. The second method is Conway's. A pentomino is a plane geometric figure formed by joining five equal squares edge to edge. It is a polyomino with five cells. There are twelve pentominoes, not counting rotations and reflections as distinct. John Horton Conway proposed an alternate labeling scheme for pentominoes, using O instead of I, Q instead of L, R instead of F, and S instead of N.
Symmetry[edit] Pentominoes have the following categories of symmetry: F, L, N, P, and Y can be oriented in 8 ways: 4 by rotation, and 4 more for the mirror image. If reflections of a pentomino are considered distinct, as they are with one-sided pentominoes, then the first and fourth categories above double in size, resulting in an extra 6 pentominoes for a total of 18. For example, the eight possible orientations of the L, F, N, P, and Y pentominoes are as follows: Tiling with rectangles. Pinwheel tiling. Pinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway.
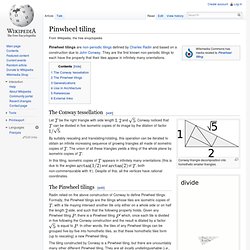
They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations. The Conway tessellation[edit] Conway triangle decomposition into homothetic smaller triangles. Let be the right triangle with side length and . Penrose tiling. A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles.
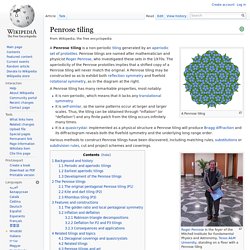
Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right.
A Penrose tiling has many remarkable properties, most notably: It is non-periodic, which means that it lacks any translational symmetry.It is self-similar, so the same patterns occur at larger and larger scales. Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings. Background and history[edit] Tiling by regular polygons. List of convex uniform tilings. This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane , and their dual tilings.
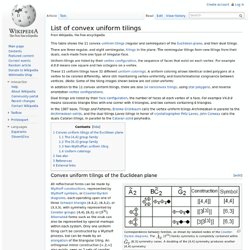
There are three regular, and eight semiregular, tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face. Uniform tilings are listed by their vertex configuration , the sequence of faces that exist on each vertex. For example means one square and two octagons on a vertex. These 11 uniform tilings have 32 different . In addition to the 11 convex uniform tilings, there are also 14 nonconvex tilings , using star polygons , and reverse orientation vertex configurations .
Aperiodic tiling. An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic patches.
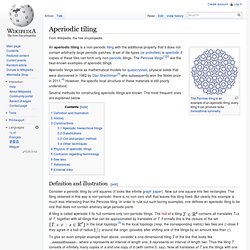
A set of tile-types (or prototiles) is aperiodic if copies of these tiles can form only non-periodic tilings. The Penrose tilings[1][2] are the best-known examples of aperiodic tilings. Aperiodic tilings serve as mathematical models for quasicrystals, physical solids that were discovered in 1982 by Dan Shechtman[3] who subsequently won the Nobel prize in 2011.[4] However, the specific local structure of these materials is still poorly understood. Several methods for constructing aperiodic tilings are known.
The most frequent ones are explained below. Definition and illustration[edit] Consider a periodic tiling by unit squares (it looks like infinite graph paper). Contains all translates T+x of T, together with all tilings that can be approximated by translates of T. -close if they agree in a ball of radius History[edit] Constructions[edit]