

What is elliptical curve cryptography (ECC)? - Definition from WhatIs.com. Elliptical curve cryptography (ECC) is a public key encryption technique based on elliptic curve theory that can be used to create faster, smaller, and more efficient cryptographic keys.
ECC generates keys through the properties of the elliptic curve equation instead of the traditional method of generation as the product of very large prime numbers. The technology can be used in conjunction with most public key encryption methods, such as RSA, and Diffie-Hellman. According to some researchers, ECC can yield a level of security with a 164-bit key that other systems require a 1,024-bit key to achieve.
Because ECC helps to establish equivalent security with lower computing power and battery resource usage, it is becoming widely used for mobile applications. ECC was developed by Certicom, a mobile e-business security provider, and was recently licensed by Hifn, a manufacturer of integrated circuitry (IC) and network security products. A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography. Elliptic Curve Cryptography (ECC) is one of the most powerful but least understood types of cryptography in wide use today.
At CloudFlare, we make extensive use of ECC to secure everything from our customers' HTTPS connections to how we pass data between our data centers. Fundamentally, we believe it's important to be able to understand the technology behind any security system in order to trust it. To that end, we looked around to find a good, relatively easy-to-understand primer on ECC in order to share with our users. Finding none, we decided to write one ourselves. The Original Magazine of the Linux Community. Elliptic Curve Public Key Cryptosystems - Alfred J. Menezes.
Public key - Why is elliptic curve cryptography not widely used, compared to RSA? RSA was there first.
That's actually enough for explaining its preeminence. RSA was first published in 1978 and the PKCS#1 standard (which explains exactly how RSA should be used, with unambiguous specification of which byte goes where) has been publicly and freely available since 1993. The idea of using elliptic curves for cryptography came to be in 1985, and relevant standards have existed since the late 1990s. Also, both RSA and elliptic curves have been covered by patents, but the RSA patents have expired in 2000, while some elliptic curve patents are still alive.
One perceived, historical advantage of RSA is that RSA is two algorithms, one for encryption and one for signatures, that could both use the same key and the same core implementation. The only scientifically established advantaged of RSA over elliptic curves cryptography is that public key operations (e.g. signature verification, as opposed to signature generation) are faster with RSA.
Elliptic curve cryptography. Elliptic curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields.
ECC requires smaller keys compared to non-ECC cryptography (based on plain Galois fields) to provide equivalent security. Elliptic curves are applicable for encryption, digital signatures, pseudo-random generators and other tasks. They are also used in several integer factorization algorithms that have applications in cryptography, such as Lenstra elliptic curve factorization.
Rationale[edit] The primary benefit promised by ECC is a smaller key size, reducing storage and transmission requirements, i.e. that an elliptic curve group could provide the same level of security afforded by an RSA-based system with a large modulus and correspondingly larger key: for example, a 256-bit ECC public key should provide comparable security to a 3072-bit RSA public key. The U.S. History[edit] Theory[edit] Cryptographic schemes[edit] World's New Largest Prime Number Discovered, Has 22 Million Digits. The new largest ever prime number has been discovered by a computer in Missouri.
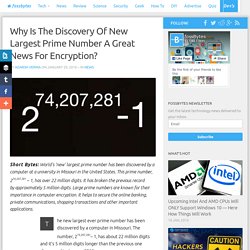
The number, 274,207,281– 1, has about 22 million digits and it’s 5 million digits longer than the previous one discovered in January 2013. Prime numbers are the numbers that are divisible by themselves and one, for example, 2,3,5,11 and 13. This new number was a result of the Great Internet Messene Prime Search (GIMPS) collaboration, which is an effort by the volunteers from all around the world to find a larger prime number. The team at the University of Central Missouri, that broke this record, also held the past record. How are world’s largest prime numbers discovered? The prime numbers written as one less than a power of two (2n – 1) are also called Mersenne primes. This search for the biggest prime numbers is conducted using a software called prime95, which is developed by GIMPS team.
Cooper and his team told the press that he was notified by an email sent by the software.