

Escala logarítmica. 6CyT 03. Escala logarítmica de frecuencia - musiki. Las escalas logarítmicas, son escalas de medida que sirven para la representación de datos que cubren una amplia gama de valores y que, para reducirlos a un rango mas manejable, utilizan el logaritmo de una cantidad física en lugar de la propia cantidad.
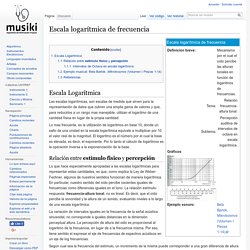
Lo mas frecuente, es la utilización de logaritmos en base 10, donde un salto de una unidad en la escala logarítmica equivale a multiplicar por 10 el valor real de la magnitud. El logaritmo es el número por el cual la base es elevada, es decir, el exponente. Por lo tanto el cálculo de logaritmos es la operación inversa a la exponenciación de la base. Relación entre estímulo físico y percepción Lo que hace especialmente apropiadas a las escalas logarítmicas para representar estas cantidades, es que, como explica la Ley de Weber-Fechner, algunos de nuestros sentidos funcionan de manera logarítmica. Según cual sea la frecuencia del estímulo, un incremento de la misma puede corresponder a una gran diferencia de altura o a una muy pequeña. Untitled Document. pH-Casa.pdf. APLICACIÓN DE LOGARITMOS EN LA MÚSICA by luzmila nina on Prezi.
Logaritmo en la vida - Google Slides. Algunas-de-las-aplicaciones-que-tienen-los-logaritmos.pdf. Aplicación de Logaritmos en la vida Diaria. APLICACIONES DE LOS LOGARITMOS EN LA VIDA REAL by P. G.García on Prezi. Aplicaciones de la funcion exponencial y logaritmica.mp4. EL BLOG DE MARIA: APLICACIÓN DE LOGARITMOS EN LA VIDA DIARIA. En matemáticas, el logaritmo de un número en una base determinada es el exponente al cual hay que elevar la base para obtener dicho número.
Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10. Navegando en un mar de números: Historia de los logaritmos. En la entrada anterior se definió el logaritmo y se expuso algunos ejemplos de sus aplicaciones.
Sin embargo, ninguno de ellos fue el motivo por el cual se descubrieron. Aunque suene chocante, los logaritmos se descubrieron como una estrategia para facilitar la multiplicación, división y raíces de números con varios decimales. El fundador de la teoría de los logaritmos y el que les dió ese nombre fue John Napier (1550-1617). Napier, además de aficionado a las matemáticas, estaba interesado en la astrología. Esto le llevó a investigar las propiedades de las figuras geométricas sobre una superficie esféricas, obteniendo importantes resultados en la resolución de triángulos esféricos. Napier se dió cuenta de algo que ya conocía Arquímedes (287 a.C. Historia : logaritmos. La importancia de medir y calcular En el s.

XVII se acomete el estudio preciso de las leyes naturales (con las funciones) y de sus variaciones (con el Cálculo Diferencial). Pero se trataba de conceptos teóricos que debían aplicarse a medidas experimentales, sobre las que luego había que realizar cálculos laboriosos. Se ponían en evidencia dos requisitos importantes: por una parte, disponer de un sistema universal de medidas; y, por otra, mejorar la capacidad de cálculo. Lo primero no se alcanza plenamente hasta 1792, cuando la Academia de Ciencias de París establece el Sistema Métrico Decimal, un triunfo imperecedero del racionalismo impuesto por la Revolución Francesa (ver grabado de la derecha).
Pero la mejora de los cálculos, tanto en rapidez como en precisión, era una línea de avance permanente desde el siglo XV, que había fructificado ya en el siglo XVI en un concepto decisivo: el logaritmo. Renacimiento: tablas para los cálculos Ahora calculamos: p67108864 = p226 = 226:2 = 213 = 819. Logaritmo. En matemáticas, el logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número.
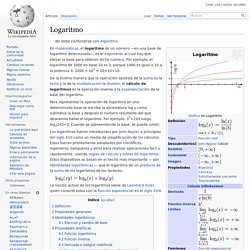
Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10. Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir. Curso gratis de Logaritmos y Ecuaciones Exponenciales - Logarítmos y Ecuaciones Exponenciales. La palabra logaritmo procede de dos palabras griegas: lógos que significa: razón,relación, manera, estilo,… y arithmós que significa número.
Los logaritmos fueron una herramienta muy importante antes de que surgieran las calculadoras científicas y los ordenadores. Anteriormente, cuando teníamos que realizar operaciones con números grandes teníamos que recurrir a los logaritmos por ejemplo, calcular: Logaritmos: ejercicios, definición y propiedades.