

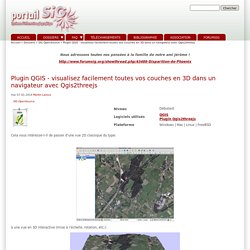
Smf gazette 147 58 61. Plugin QGIS - visualisez facilement toutes vos couches en 3D dans un navigateur avec Qgis2threejs. Cela vous intéresse-t-il de passer d'une vue 2D classique du type: à une vue en 3D interactive (mise à l'échelle, rotation, etc.
Une Minute Pour Comprendre. Découvrez le livre de l'auteur, Le Beau Livre des maths. Open mathematics. The biggest mystery in mathematics: Shinichi Mochizuki and the impenetrable proof. Illustration by Paddy Mills Sometime on the morning of 30 August 2012, Shinichi Mochizuki quietly posted four papers on his website.

The papers were huge — more than 500 pages in all — packed densely with symbols, and the culmination of more than a decade of solitary work. They also had the potential to be an academic bombshell. In them, Mochizuki claimed to have solved the abc conjecture, a 27-year-old problem in number theory that no other mathematician had even come close to solving. If his proof was correct, it would be one of the most astounding achievements of mathematics this century and would completely revolutionize the study of equations with whole numbers.
Jean Mawhin, Calcul des variations et mécanique analytique chez Lagrange.