

Teorema de Pitágoras. Teorema de Pitágoras - Definición, fórmula, ejemplos, ejercicios y demostración. TEOREMA DE PITAGORAS. Teorema de Pitágoras generalizado Si en vez de construir un cuadrado, sobre cada uno de los lados de un triángulo rectángulo, construimos otra figura, ¿seguirá siendo cierto, que el área de la figura construida sobre la hipotenusa es igual a la suma de las áreas de las figuras semejantes construidas sobre los catetos? (Pinchando en los dibujos siguientes se accede a la comprobación numérica en las figuras que se representan) A lo largo de la historia han sido muchas las demostraciones y pruebas que matemáticos y amantes de las matemáticas han dado sobre este teorema. Se reproducen a continuación algunas de las más conocidas. A continuación se presentan algunas demostraciones visuales del teorema de Pitágoras en forma de puzzles. 1.- Los siguientes disecciones son válidas para cualquier triángulo rectángulo.
Se han ordenado de menos a mayor número de piezas que lo forman. 2.- Los puzzles siguientes sólo son validos en el caso de que el triángulo rectángulo inicial sea el que se indica. Teorema de Tales. Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a.
C. El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente ( triángulos semejantes son los que tienen iguales ángulos ). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa ). Primer teorema. Razón y proporción. Resolución de problemas por medio de la proporción Uno de los tipos de problemas basados en proporciones implica triángulos con lados proporcionales.

Supongamos que se sabe que los lados correspondientes de dos triángulos son proporcionales. (Ver figura 13 1.) Las longitudes de los lados de un triángulo son 8, 9 y 11. La longitud del lado del segundo triángulo correspondiente al lado 8, en el primer triángulo, es 10. FIGURA 13-1. Visto que los lados correspondientes son proporcionales, los pares de lados correspondientes se usarán para formar las proporciones, de esta manera: A fin de resolver para b usamos la proporción y obtenemos el siguiente resultado: La solución para c es similar a aquella para b, empleando la proporción con el resultado que sigue: Los lados del segundo triángulo son 10, 11 1/4 y 13 3/4. El factor de proporcionalidad es entonces 5/4. Triángulos semejantes. Dados los triángulos ABC y A'B'C' determinamos los lados y ángulos homólogos.
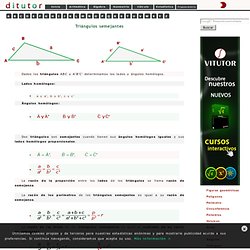
Lados homólogos: a y a', b y b', c y c' Triángulos congruentes. Definición de Congruencia. En la geometría euclidiana, la congruencia es fundamental; es lo equivalente a igualdad matemática en aritmética y álgebra.
En geometría analítica, la congruencia puede ser definida así: dos figuras determinadas por puntos sobre un sistema de coordenadas cartesianas son congruentes si y solo si, para cualquier par de puntos en la primera figura, la distancia euclidiana entre ellos es igual a la distancia euclidiana entre los puntos correspondientes en la segunda figura. Una definición más formal: dos subconjuntos A y B de un espacio euclídeo Rn son llamados congruentes si existe una isometría f : Rn → Rn (un elemento del grupo euclideo E(n)) con f(A) = B. Los ángulos opuestos por el vértice son un ejemplo de ángulos congruentes. Las diagonales de un paralelogramo configuran ángulos opuestos por el vértice congruentes. La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos y lados de igual medida o congruentes. Criterios de congruencia. Observa los siguientes triángulos: Al mirar los dos pares de triángulos se puede apreciar que en ambos los triágulos tienen entre si la misma forma y tamaño.

Propiedades de los triángulos. Propiedades de los triángulos isósceles - Euclides. Propiedades Para demostrar varias propiedades del triángulo isósceles, trazaremos la bisectriz del ángulo opuesto a la base.
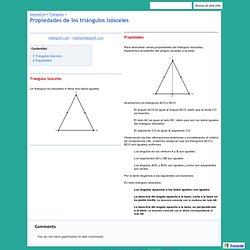
Analicemos los triángulos ACO y BCO. El ángulo ACO es igual al ángulo BCO, dado que la recta CO es bisectriz.El lado AC es igual al lado BC, dado que son los lados iguales del triángulo isósceles.El segmento CO es igual al segmento CO. Observando las tres afirmaciones anteriores y considerando el criterio de congruencia LAL, podemos asegurar que los triángulos ACO y BCO son iguales, entonces: Ángulos en un triángulo. Como elaborar un Triángulo Escaleno. Como elaborar un triángulo Escaleno. Clasificación de triángulos.