

«Optimalité : choix, contraintes, hasard.» un thème où l’on retrouve la déraisonnable efficacité des mathématiques grâce à l’informatique. — Pixees. Trois mots clés qui se fédèrent en une théorie.

©IHP – Maison des mathématiques. Les mathématiques se mettent au service de problèmes concrets pour produire grâce à l’informatique, les meilleures solutions. Choix. Pour faire un choix, pour prendre une décision, il faut clairement disposer d’informations et d’une représentation (ou “modèle”) de la situation qui réclame ce choix. Une question ? Contactez-nous ! Jeux à champ moyen : définition wikipédia. Gestion des stocks et de la production intégrant des retours de produits : thèse de Samuel Vercraene, 2012.
Abstract : Flows of returns due to recycling and reusing waste are developing in order to preserve the limited natural resources of our planet.
These new flows interact with the traditional production flows. Therefore, in order to provide customers with the best service level and minimize the stock in the supply chain, the control of the return flows appears to be of highest importance. We address this problem by modeling a situation with a limited porduction capacity and we consider an operational production/inventory problem that incorporates flows of returns.
We model three continuous-time production/inventory problems with limited produc- tion capacities, random lead times, and linear costs. Mean field games : T. Tao, 2010 [en anglais] John Nash, la théorie des jeux et la question du bon choix : article du Monde, mai 2013. Le mathématicien et prix Nobel John Forbes Nash est mort à l'âge de 86 ans.
L'occasion de revenir sur sa spécialité, la théorie des jeux. LE MONDE SCIENCE ET TECHNO | • Mis à jour le | Philippe Pajot Le mathématicien américain John Forbes Nash est mort à l'âge de 86 ans. Ci-dessous, un article datant de mai 2013 où il est question de sa spécialité, la théorie des jeux. Cours de Pierre-Louis Lions au Collège de France. Apprentissage automatique et Big Data : Simon Lacoste-Julien, 2014. Algorithmique du style : de nouveaux espaces pour la composition et l’improvisation : François Pachet, 2015. Les jeux à champ moyen - Brèves de Maths, 2013. Équilibre de Nash, inventeur du jeu de Hex : Brèves de maths, 2013. John Forbes Nash, Jr.

John Forbes Nash Jr est né en 1928 à Bluefield aux États-Unis, en Virginie-Occidentale. Poussé par ses enseignants sur la voie des mathématiques, il prépare une thèse à l’université de Princeton. Durant ces années, il a inventé le jeu de hex pour la salle commune des élèves et des professeurs. Richard Bellman et la programmation dynamique - Brèves de Maths, 2013. Richard Bellman (1920-1984).
Richard Bellman est né le 26 août 1920 à New York. Créer de nouvelles routes peut générer davantage d’embouteillages ou le paradoxe de Braess-Brèves de Maths, 2013. La très fréquentée 42ème rue de New York.
Sa fermeture à la circulation en 1990 a, contre toute attente, fluidifié la circulation. Le prix de l'anarchie ou le paradoxe de Braess, Étienne Ghys, 2009. Deux paradoxes Pour expliquer cela, nous allons commencer par décrire un autre phénomène découvert par A.C.

Pigou — un économiste — en 1920 [2]. Supposons que deux villes et , de part et d’autre d’un fleuve, soient reliées par deux routes. La première est excellente, très large, mais elle fait malheureusement un grand détour : il faut une heure pour la parcourir, et ceci quel que soit le nombre de véhicules qui l’empruntent (dans des limites raisonnables, par exemple jusqu’à 1000 véhicules par heure). Dossier thématique sur transport optimal dans Images des mathématiques. Les mathématiques, la clé d'un trafic fluide ? - 31/07/2015 - ladepeche.fr.
Si vous prenez la route ce week-end à l'occasion du grand chassé-croisé de l'été et que les centaines de kilomètres de bouchons attendus vous angoissent, rassurez-vous: des mathématiciens tentent d’alléger vos souffrances en définissant des systèmes de régulation du trafic.
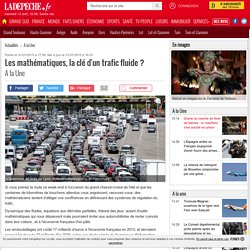
Dynamique des fluides, équations aux dérivées partielles, théorie des jeux: autant d'outils mathématiques qui nous dépassent mais pourraient éviter aux automobilistes de rester coincés dans leur voiture...et à l'économie française d'en pâtir. Les embouteillages ont coûté 17 milliards d’euros à l'économie française en 2013, et devraient peser à hauteur de 22 milliards d'ici 2030, selon une étude signée du fournisseur d'information routière INRIX et du Centre for Economics and Business Research (Cebr). Soit plus que le trou de la Sécu en 2014. Création d'un Inria Innovation Lab pour réduire la consommation en carburant des avions.
Partenariat Recherche - Industrie Le partenariat entre Safety Line et l’équipe de recherche COMMANDS se concrétise aujourd’hui par la création d’un Inria Innovation Lab.
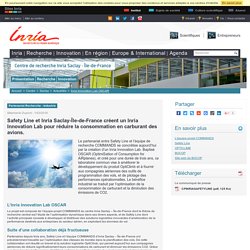
Baptisé OSCAR (OptimiSation of Consumption for AiRplanes), et créé pour une durée de trois ans, ce laboratoire commun vise à améliorer le développement du produit OptiClimb et à fournir aux compagnies aériennes des outils de programmation des vols, et de pilotage des performances opérationnelles. Convexité et optimisation : cours de Guy Cohen, 2000, corr. 2006. Optimisation et apprentissage : Alexandre d'Aspremont, 2014. La programmation par contraintes expliquée à ma garagiste ou à mon fleuriste : Charlotte Truchet, 2015. Parmi les grandes familles d'approches et de langages informatiques, on entend parfois parler de « programmation par contraintes ».
Un chercheur du domaine vous expliquerait peut-être que « c'est un paradigme de programmation déclarative permettant de traiter des problèmes fortement combinatoires ». La programmation par contraintes : Étienne Parizot, Sylvain Soliman, François Fages, 2004. Lorsque les contraintes sont nombreuses, la résolution d'un problème est en pratique très difficile. Surtout si on exige de trouver la meilleure solution possible... © potowizard - Fotolia.com Supposons qu'on veuille organiser la rotation des avions dans un aéroport, en optimisant l'utilisation des pistes, l'emploi du temps du personnel navigant, l'attente des voyageurs, l'acheminement des bagages, etc.
Optimisation : quand le mieux n'est pas l'ennemi du bien : conférence Pierre Martinon, 2009. Conception interactive d’environnements urbains durables à base de résolution de contraintes : thèse de Bruno Belin, 2014. Abstract : The design of more sustainable cities has emerged as a central society issue. Publications dans les conférences JFPC (Journées Francophones de Programmation par Contraintes) Search. Colisweb améliore son modèle de livraison avec Inria. Collaboration © Colisweb C’est un problème complexe que Colisweb a soumis à l’équipe Inocs d’Inria Lille - Nord Europe : déterminer à l’avance le planning d’une flotte de livreurs, sans connaître leur charge de travail.
Algorithme génétique : définition wikipédia. Origines[modifier | modifier le code] La popularisation des algorithmes génétiques sera l'œuvre de David Goldberg à travers son livre Genetic Algorithms in Search, Optimization, and Machine Learning[1] (1989). Le hasard fait bien les choses : exposé de Corinne Touati (vidéo 1), 2013. Le hasard fait bien les choses : 1ère partie Cet exposé porte sur la "théorie des jeux" ou, plus simplement, "comment modéliser un système mettant en jeu des acteurs en interaction? ". Nous montrons tout d'abord quelques exemples introductifs à la théorie des jeux et les éventuelles conséquences néfastes de la multiplication des preneurs de décisions en terme d'efficacité globale.
Dans une seconde partie, nous présentons succinctement quelques applications de ces phénomènes dans des problèmes de ressources dans les réseaux de télécommunication et montrons notamment au travers du problème d'association entre mobiles (téléphone, ordinateur...) et stations de base (antenne du fournisseur d'accès) dans les réseaux sans-fils comment l'ajout de hasard dans la prise de décision permet d'aboutir à des allocations optimales.
Le hasard fait bien les choses : exposé de Corinne Touati (vidéo 2), 2013. Le hasard fait bien les choses : 2ème partie Cet exposé porte sur la "théorie des jeux" ou, plus simplement, "comment modéliser un système mettant en jeu des acteurs en interaction? ". Nous montrons tout d'abord quelques exemples introductifs à la théorie des jeux et les éventuelles conséquences néfastes de la multiplication des preneurs de décisions en terme d'efficacité globale. Dans une seconde partie, nous présentons succinctement quelques applications de ces phénomènes dans des problèmes de ressources dans les réseaux de télécommunication et montrons notamment au travers du problème d'association entre mobiles (téléphone, ordinateur...) et stations de base (antenne du fournisseur d'accès) dans les réseaux sans-fils comment l'ajout de hasard dans la prise de décision permet d'aboutir à des allocations optimales.
Le hasard fait bien les choses : Denis Talay, 2009. Comme je suis un spécialiste de la théorie des probabilités (version courte : un probabiliste), mon expression favorite est « le hasard fait bien les choses ». Je me propose d’en commenter ici deux sens différents à l’aide de concepts probabilistes (plus ou moins) élémentaires. Le premier sens de mon expression favorite est celui du langage courant : on indique ainsi qu’un évènement heureux, bien qu’inattendu, s’est produit. Mais que signifie-t-on exactement ? A la réflexion, la locution est complexe : les mots « hasard » et « faire » semblent s’opposer, l’un suggérant une absence de volonté et de destin, l’autre sous-entendant une intention : il m’est arrivé quelque chose d’heureux sans que je l’aie provoqué ; c’est le hasard qui en a décidé ainsi.
Le second sens de « le hasard fait bien les choses » recouvre une réalité mathématique et numérique : le hasard rend de fabuleux services. La conquête du hasard : Fernando Corbalán, Gerardo Sanz, 2013. Introduction à la théorie des jeux : Sébastien Konieczny. Les mathématiques de l'évolution : documentaire de Régis Ferrière. Hasard et chance du 27 juin 2016 - France Inter. Peut-on calculer le hasard ? France culture 8/12/2016. Références bibliographiques.