

Reseau bay�sien. Arbre bicolore. Un article de Wikipédia, l'encyclopédie libre.
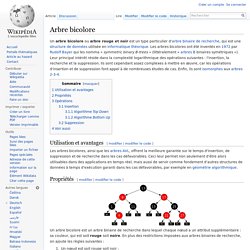
Un arbre bicolore ou arbre rouge et noir est un type particulier d'arbre binaire de recherche, qui est une structure de données utilisée en informatique théorique. Les arbres bicolores ont été inventés en 1972 par Rudolf Bayer qui les nomma « symmetric binary B-trees » (littéralement « arbres B binaires symétriques »). Leur principal intérêt réside dans la complexité logarithmique des opérations suivantes : l'insertion, la recherche et la suppression. Ils sont cependant assez complexes à mettre en œuvre, car les opérations d'insertion et de suppression font appel à de nombreuses études de cas. Enfin, ils sont isomorphes aux arbres 2-3-4. Utilisation et avantages[modifier | modifier le code] Les arbres bicolores, ainsi que les arbres AVL, offrent la meilleure garantie sur le temps d'insertion, de suppression et de recherche dans les cas défavorables.
Propriétés[modifier | modifier le code] La propriété 2 n'est pas nécessaire. Université de Liège - Mathématiques Discrètes. DCMI Metadata Terms. Table of Contents Index of Terms Section 1: Introduction and Definitions This document is an up-to-date, authoritative specification of all metadata terms maintained by the Dublin Core Metadata Initiative.

Included are the fifteen terms of the Dublin Core Metadata Element Set, which have also been published as IETF RFC 5013 [RFC5013], ANSI/NISO Standard Z39.85-2007 [NISOZ3985], and ISO Standard 15836:2009 [ISO15836]. Each term is specified with the following minimal set of attributes: Where applicable, the following attributes provide additional information about a term: This release of DCMI Metadata Terms reflects changes described more fully in the document "Maintenance changes to DCMI Metadata Terms" [REVISIONS].
References Section 2: Properties in the /terms/ namespace Section 3: Properties in the /elements/1.1/ namespace Section 4: Vocabulary Encoding Schemes Section 5: Syntax Encoding Schemes Section 6: Classes Section 7: DCMI Type Vocabulary Errata: Mathématiques 1re année MPSI Tout en un - Xavier Oudot, Marie Allano-Chevalier. Mathématiques 1re année MPSI Tout en un - Xavier Oudot, Marie Allano-Chevalier. Les probabilités et la statistique de A à Z - 500 définitions, formules et ... - François Dress. FLOT : Réviser l’algèbre. Anneaux. P=NP? Théorie des ensembles.
Application linéaire-Injectivité, surjectivité, bijectivité. Mathématiques Espaces vectoriels Application linéaire Précédent Suivant Théorème Soient et deux espaces vectoriels sur un même corps .

De type fini et soit n sa dimension. Une base de une application linéaire de dans . Chacune des propriétés intervenant dans cet énoncé est une condition nécessaire et suffisante ; la preuve des deux premières sera donc décomposée en deux parties, la troisième s'en déduisant immédiatement. Preuve : Preuve du 1 est injective est une famille libre de . Preuve : Preuve du 2 est surjective engendre L'hypothèse surjective signifie que .Or on a vu dans la proposition que si est une base de , est une famille de générateurs de .Donc engendre .
Preuve : Preuve du 3 est un isomorphisme de sur est une base de .Cette équivalence résulte immédiatement des points et . Conséquence immédiate dans le cas où F est aussi de type finie Corollaire : Corollaire 1 deux espace vectoriels sur un même corps de type fini. Alors est de type fini et Ce résultat est immédiat si . Avec deux. Algèbre linéaire I. Dimension d'un espace vectoriel. Calculus One - On-demand Course. Math. Mathematics. Mathematics.