

Set symbols of set theory (Ø,U,{},∈,...) Earth's magnetic field. Computer simulation of the Earth's field in a period of normal polarity between reversals.[1] The lines represent magnetic field lines, blue when the field points towards the center and yellow when away.
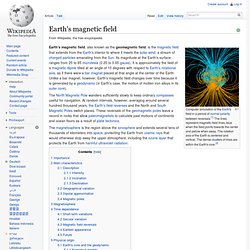
The rotation axis of the Earth is centered and vertical. The dense clusters of lines are within the Earth's core.[2] The North Magnetic Pole wanders sufficiently slowly to keep ordinary compasses useful for navigation. At random intervals, however, averaging around several hundred thousand years, the Earth's field reverses and the North and South Magnetic Poles switch places. These reversals of the geomagnetic poles leave a record in rocks that allow paleomagnetists to calculate past motions of continents and ocean floors as a result of plate tectonics. Magnetic dipole. Dipole moment m.
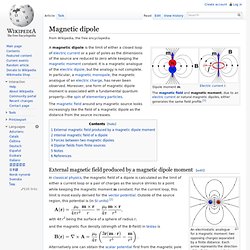
The magnetic field around any magnetic source looks increasingly like the field of a magnetic dipole as the distance from the source increases. External magnetic field produced by a magnetic dipole moment[edit] An electrostatic analogue for a magnetic moment: two opposing charges separated by a finite distance. Magnetic moment. The magnetic moment of a magnet is a quantity that determines the torque it will experience in an external magnetic field.
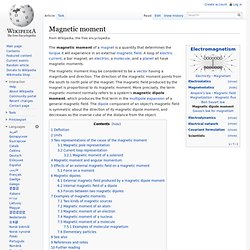
A loop of electric current, a bar magnet, an electron, a molecule, and a planet all have magnetic moments. Definition[edit] The magnetic moment is defined as a vector relating the aligning torque on the object from an externally applied magnetic field to the field vector itself. The relationship is given by [1] where. Magnetic Field of a Current Loop. Integral. A definite integral of a function can be represented as the signed area of the region bounded by its graph.
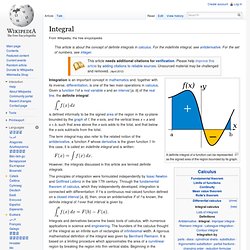
The term integral may also refer to the related notion of the antiderivative, a function F whose derivative is the given function f. In this case, it is called an indefinite integral and is written: However, the integrals discussed in this article are termed definite integrals. The principles of integration were formulated independently by Isaac Newton and Gottfried Leibniz in the late 17th century. Integral (calculus) - RapidTables.com. The Gamma Function The Gamma function is convergent for x>0.
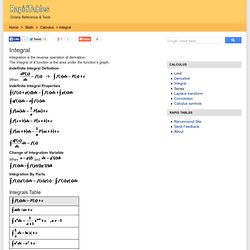
Gamma Function Properties G(x+1) = xG(x) G(n+1) = n! , when nℕ (positive integer). The Beta Function Beta Function and Gamma Function Relation. Constant of integration. The Analyst. The Analyst, subtitled "A DISCOURSE Addressed to an Infidel MATHEMATICIAN.
WHEREIN It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith", is a book published by George Berkeley in 1734. The "infidel mathematician" is believed to have been Edmond Halley, though others have suggested Sir Isaac Newton was intended. (Burton 1997, 477) Background and purpose[edit] Alciphron was widely read and caused a bit of a stir.
1202.4153v1. Edmond Halley. Edmond Halley, FRS (commonly misspelt as Edmund,[2] pronounced /ˈɛdmənd ˈhæli/;[3][4] 8 November 1656 – 14 January 1742) was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet.
He was the second Astronomer Royal in Britain, succeeding John Flamsteed. Early life[edit] Halley was born in Haggerston, Shoreditch, England. His father, Edmond Halley Sr., came from a Derbyshire family and was a wealthy soap-maker in London. As a child, Halley was very interested in mathematics. Career[edit] Publications and inventions[edit] Actuarial science. Demography. “Demo-” from Ancient Greek δῆμος dēmos, means “the people” and “-graphy” from γράφω graphō, means “measurement.”[1] Demographic analysis can be applied to whole societies or to groups defined by criteria such as education, nationality, religion and ethnicity.
Institutionally, demography is usually considered a field of sociology, though there are a number of independent demography departments.[2] Formal demography limits its object of study to the measurement of populations processes, while the broader field of social demography population studies also analyze the relationships between economic, social, cultural and biological processes influencing a population.[3] The term demographics refers to characteristics of a population. Methods[edit] There are two types of data collection — direct and indirect — with several different methods of each type. Direct methods[edit] A census is the other common direct method of collecting demographic data. Censuses do more than just count people. Calculus symbols list (ε, y', d/dx , ∫) Line integral. Biot-Savart Law. Magnetic Concepts. Multipole expansion. Expansion in spherical harmonics[edit]
Cross product. If the vectors have the same direction or one has zero length, then their cross product is zero.
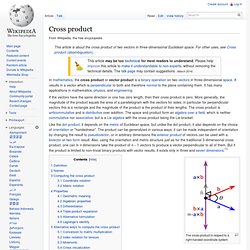
More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular for perpendicular vectors this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative and is distributive over addition. The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.
The cross-product in respect to a right-handed coordinate system. Lie algebra. In mathematics, Lie algebras (/ˈliː/, not /ˈlaɪ/) are algebraic structures which were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" (after Sophus Lie) was introduced by Hermann Weyl in the 1930s.
In older texts, the name "infinitesimal group" is used. Related mathematical concepts include Lie groups and differentiable manifolds.