

From order to randomness. One of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002).
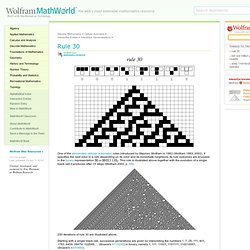
It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55). 250 iterations of rule 30 are illustrated above. Starting with a single black cell, successive generations are given by interpreting the numbers 1, 7, 25, 111, 401, 1783, 6409, 28479, 102849, ... Rule 30 is the mirror image, complement, and mirror complement of rules 86, 135, and 149, respectively. Rule 30 is of special interest because it is chaotic (Wolfram 2002, p. 871), with central column given by 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ...
Jen (1990) proved that with the initial state of a single black cell, the sequence of colors attained in any two adjacent cells is not periodic (Gray 2003). Golly Game of Life Home Page. John Conway's Game of Life. The Game The Game of Life is not your typical computer game.
It is a 'cellular automaton', and was invented by Cambridge mathematician John Conway. This game became widely known when it was mentioned in an article published by Scientific American in 1970. It consists of a collection of cells which, based on a few mathematical rules, can live, die or multiply. Depending on the initial conditions, the cells form various patterns throughout the course of the game. playgameoflife.com New developments of this page will continue on playgameoflife.com. Elementary Cellular Automaton. The simplest class of one-dimensional cellular automata.
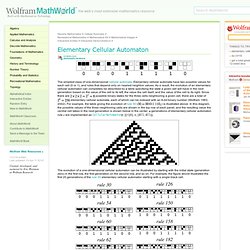
Elementary cellular automata have two possible values for each cell (0 or 1), and rules that depend only on nearest neighbor values. As a result, the evolution of an elementary cellular automaton can completely be described by a table specifying the state a given cell will have in the next generation based on the value of the cell to its left, the value the cell itself, and the value of the cell to its right. Since there are possible binary states for the three cells neighboring a given cell, there are a total of elementary cellular automata, each of which can be indexed with an 8-bit binary number (Wolfram 1983, 2002). ) is illustrated above. Generations of elementary cellular automaton rule are implemented as CellularAutomaton[r, , n, All, All The illustrations above show some automata numbers that give particularly interesting pattern propagated for 15 generations starting with a single black cell in the initial iteration.