Statistics

The Mean from a Frequency Table. Bayes’ Theorem with Lego. Solve My Maths. An Average Problem. I’ve lost a Dime. I haven’t actually lost a dime, rather I’m missing a Dime – specifically the second Dime probability pack.

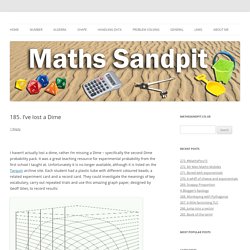
It was a great teaching resource for experimental probability from the first school I taught at. Unfortunately it is no longer available, although it is listed on the Tarquin archive site. Each student had a plastic tube with different coloured beads, a related experiment card and a record card. They could investigate the meanings of key vocabulary, carry out repeated trials and use this amazing graph paper, designed by Geoff Giles, to record results: The graph paper works a little like a bagatelle or pinball machine. Activity I decided to recreate the old Dime investigation sheets: Students start by explaining what their experiment is and define what is a success/fail. Students then carry out their experiment, recording their results in the tally chart and graph.

Download the worksheet here: Experimental Probability investigation Sample. Standardised Normal Distribution [Hinge Questions] This post is to check understanding of normal distributions when students are required to standardise.

Note that the answers given are from using the normal table to look up P(Z < z), not a calculator method. a) The student mixed their units and so ended up with an incorrect z value b) Correct answer c) Student used the standardised value as the probability d) Student made an error in the standardising formula (rather than X – μ, student did μ – X) e) Student looked up the value given (1.45) rather than standardising In case you wondered; this is for a different class ;-) Like this: Like Loading...

This entry was posted in Classroom, General Maths Thoughts, Hinge Questions, Lessons, Pedagogy and tagged Conferences, General Maths Thoughts, Hinge Questions, Lessons, Pedagogy, Statistics. Histograms (TLP) 1.

(Below) Drawing and Reading Histograms 2. (Below) Pret Homework 3. 140. Cut out the Quartiles. Quartiles on cumulative frequency graphs are such easy questions when you get ‘it’.

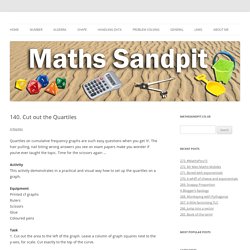
The hair pulling, nail biting wrong answers you see on exam papers make you wonder if you’ve ever taught the topic. Time for the scissors again … Activity This activity demonstrates in a practical and visual way how to set up the quartiles on a graph. Equipment Printed cf graphs Rulers Scissors Glue Coloured pens Task 1. 2. Repeat the half fold again 3. 4. 5. 6. 7. 8. Review This activity covers a fair few learning styles and creates a visual/memorable resource,in their books. One-Die Toss Activities. Continuous Everywhere but Differentiable Nowhere. Matt Enlow (math teacher in MA) posted a fascinating problem online today, one he thinks of when storing all those plastic bags from the grocery store.

You shove them so they all lie in a single bag, and throw that bag under the sink. Here’s the question: how many different ways can you store these bags? For 1 bag, there is only 1 way. For 2 bags, there is still only 1 way. For 3 bags, there are 2 ways. Here is a picture for clarification: Can you figure out how many ways for 6 bags? You are now officially nerdsniped. A number of people had trouble calculating 4 bags correctly, so I’ll post the number of ways 4 bags could be stored after the jump at the bottom, so you can at least see if you’re starting off correctly… Additional Information: Matt and I figured the solution to this problem together on twitter.

Obviously I’m being purposefully vague so I don’t give anything away. Update late in the evening: It might just be Matt and my solution is wrong. Misleading Statistics: How Visual Data Can Go Bad. Understanding Probability Could Save Your LIfe. BBC iWonder - What's the maths behind a dream FA Cup draw? Measures of Spread. Cricketing MMM. Money Duck - 101qs. Tree Diagrams and Binomial Distribution. Binomial Reverse. Double or Add.

The Binomial Mean and Variance. Conditional Probability (TLP) Solve My Maths Search you're reading...

Conditional Probability, Probability, Resources Conditional Probability (TLP) Posted by solvemymaths ⋅ ⋅ Leave a comment Below: Odds and Evens Activity Below: False Positive Below: Conditional Probability Puzzler False Positives (article) Below: Bayes’ Theorem with Lego MARS Resources 1 MARS Resources 2 About these ads Share this: Like this: Related #mathsTLP 12th April 2015In "#mathsTLP" Understanding Probability Could Save Your LIfeIn "AND / OR Rules" Zombie Probability TreesIn "Data & Measure" « Rounding and Significant Figures (TLP) Tessellation (TLP) » Discussion No comments yet.

Leave a Reply Recent Posts Follow me on Twitter Solve My Maths Blog at WordPress.com. Follow Get every new post delivered to your Inbox. Join 4,560 other followers Build a website with WordPress.com. Plotly.