

Resourceaholic: Introducing Algebra. Building a solid conceptual understanding of algebra is absolutely fundamental.
As with fractions, it's essential that we get it right because it underpins so much of what follows. But, as with fractions, pupils can really struggle here. Sometimes good teaching resources inspire us when we're looking for ways to structure and deliver our teaching. This post contains some recommendations that may give you food for thought when you’re planning your lessons. Resourceaholic: 5 Maths Gems #33. Hello and welcome to my 33rd gems post.
This is where I share five teaching ideas I've seen on Twitter. Well it's been fun teaching in this week's heatwave hasn't it?! I long for an air-conditioned classroom. Still, all this lovely sunshine serves as a nice reminder that the summer holidays are just around the corner. Resourceaholic: New GCSE: Tangents and Areas. At first glance it appears that calculus features in the new GCSE specification.
On closer inspection it turns out that our students will find the gradient of a curve by drawing a suitable tangent rather than by differentiating. And instead of integrating, students will use the trapezium rule (or similar) to find the area under a curve. So calculus remains reserved for Key Stage 5, but our students will now be better prepared for calculus when they first meet it. GCSE will have given them a conceptual understanding of rate of change and an ability to interpret this contextually. Resourceaholic: New GCSE: Sequences.
I've been busy getting my head around the additional sequences content in the new 9 - 1 Maths GCSE and thought it would be helpful to share my findings.

Quite a lot has been added to the higher tier. Previously students covered all the GCSE sequences content at Key Stage 3 so there was nothing new to teach at Key Stage 4. Following on from my last post on ideas for the first Year 7 lesson of the year, here's some ideas for the start of Year 12.
Unfortunately we don't really have any time to spare in our sixth form teaching. It's a challenge just to fit enough lessons into the school year to cover all the course material before our students go off to take their exams. So, sadly, there's no time for enrichment or getting to know each other - students have to hit the ground running. Entry Assessment At my school, as at many others, we ask our students to prepare for Year 12 by doing some summer work. We expect them to have a solid understanding of GCSE topics when they start the course, particularly surds, indices and algebra. The results from our entry assessments were rather worrying. Resourceaholic: Favourite Problems. On Tuesday 23rd June I'm hosting a #mathscpdchat entitled "Problem solving: what are 'good' problems?
Where can you find them? ". What's a Problem? A problem, in the mathematical sense, can be defined as "an inquiry starting from given conditions to investigate or demonstrate a fact, result, or law". The word originated in the late 14th century,'a difficult question proposed for solution', from Old French problème, and directly from Latin problema, from Greek problema 'a task, that which is proposed, a question' (source: etymonline). I like this quote from Jennifer Piggot, "A problem is something that you probably will not immediately see how to tackle or which once started will challenge your thinking.
Resourceaholic: 5 Maths Gems #35. Hi there.
Welcome to my 35th gems post. This is where I share five teaching ideas I've seen on Twitter. The summer holidays are now in full swing so Twitter has been quiet this week. I expect it will get busier in August - results days will give us lots to talk about, and then we'll all start making preparations for September. I'm off on a family holiday next week (including an exciting day out at Peppa Pig World!) 1. @mathninja3 suggested putting a permanent angle chase on the classroom wall. 2. This week Nikki (@mathszest) tweeted a picture of her fantastic presentation guide, which she has recently updated with target codes (inspired by @letsgetmathing's conference presentation about marking). 3. In general people (not just young people) aren't very good at understanding the graphs they see in the media.
I'm not sure whether this should sit in maths or somewhere else, but I think these activities are valuable. 5 Maths Gems #35. Resourceaholic: New GCSE: Inequalities. The new GCSE specification has two additions under the heading Inequalities: a) using set notation to represent solutions b) solving quadratic inequalities.
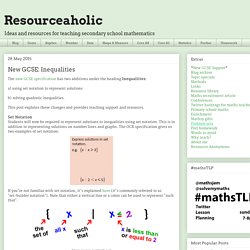
This post explains these changes and provides teaching support and resources.Set Notation Students will now be required to represent solutions to inequalities using set notation. This is in addition to representing solutions on number lines and graphs. Resourceaholic: Thoughts on Teaching Fractions. Yuvraj (@YuviLite) asked me to write a post about teaching fraction addition.

I like a challenge! Fractions are notoriously difficult to teach, riddled with misconceptions and crucial to get right. Resourceaholic: 5 Maths Gems #31. Resourceaholic: Core A2. Pages This Blog Core A2 This page lists recommended resources for teaching Core Mathematics at A2, organised by topic.Huge thanks to all individuals and organisations who share teaching resources.Algebra Functions Graph Transformations Parametric Functions Logs and Exponentials Trigonometry Differentiation Integration VectorsGeneralRevision If you find any broken links please email resourceaholic@gmail.com.
Home. Core AS. This page lists recommended resources for teaching Core Mathematics at AS level, categorised by topic. Huge thanks to all individuals and organisations who share teaching resources.Indices Graphs and FunctionsArithmetic ProgressionsRecurrence Relations Worksheet - chuckieirish on TESCoordinate Geometry - Linear Graphs DifferentiationIntegration Factor Theorem Geometric Progressions.
Resourceaholic: Tricks and Tips 1: HCF. I recently presented a workshop at the National Mathematics Teacher Conference (#mathsconf2015) entitled 'Tricks and Tips: Clever Methods for Explaining Mathematical Concepts'. This post summarises the content of that workshop for those who were unable to attend. I have quite a lot to cover so I expect I'll need to write three or four blog posts.
In this one I'm going to explain the rationale for the workshop and describe alternative methods for finding a Highest Common Factor. In subsequent posts I'll cover sequences, linear graphs, surds, quadratics, compound measures and a few more bits and pieces. Workshop aim How do you find the Highest Common Factor of two numbers? What determines the way we choose the explain things? Most teachers establish teaching habits during their training and NQT year.