

Un article de Wikipédia, l'encyclopédie libre.
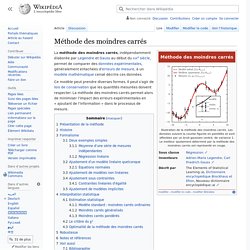
Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des moindres carrés est représenté en rouge. La méthode des moindres carrés, indépendamment élaborée par Legendre et Gauss au début du xixe siècle, permet de comparer des données expérimentales, généralement entachées d’erreurs de mesure, à un modèle mathématique censé décrire ces données.
Ce modèle peut prendre diverses formes. Présentation de la méthode[modifier | modifier le code] Dans le cas le plus courant, le modèle théorique est une famille de fonctions d’une ou plusieurs variables muettes x, indexées par un ou plusieurs paramètres inconnus. Méthode des moindres carrés. Analyse en composantes principales. Analyse en composantes principales L'analyse en composantes principales (ACP ou PCA en anglais pour principal component analysis), ou selon le domaine d'application la transformation de Karhunen–Loève (KLT)[1], est une méthode de la famille de l'analyse des données et plus généralement de la statistique multivariée, qui consiste à transformer des variables liées entre elles (dites « corrélées » en statistique) en nouvelles variables décorrélées les unes des autres.
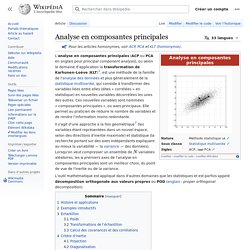
Ces nouvelles variables sont nommées « composantes principales », ou axes principaux. Elle permet au praticien de réduire le nombre de variables et de rendre l'information moins redondante. variables aléatoires, les premiers axes de l'analyse en composantes principales sont un meilleur choix, du point de vue de l'inertie ou de la variance. Histoire et applications[modifier | modifier le code] Un article de Wikipédia, l'encyclopédie libre.
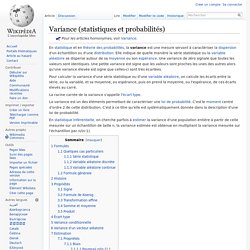
Pour les articles homonymes, voir Variance. En statistique et en théorie des probabilités, la variance est une mesure servant à caractériser la dispersion d'un échantillon ou d'une distribution. Elle indique de quelle manière la série statistique ou la variable aléatoire se disperse autour de sa moyenne ou son espérance. Une variance de zéro signale que toutes les valeurs sont identiques. Une petite variance est signe que les valeurs sont proches les unes des autres alors qu'une variance élevée est signe que celles-ci sont très écartées.
Pour calculer la variance d'une série statistique ou d'une variable aléatoire, on calcule les écarts entre la série, ou la variable, et sa moyenne, ou espérance, puis on prend la moyenne, ou l'espérance, de ces écarts élevés au carré. La racine carrée de la variance s'appelle l'écart type. Si la série statistique est de moyenne m et prend les valeurs x1, x2, ..., xn, sa variance est , existe. Variance (statistiques et probabilités) Écart type. Exemple de deux échantillons ayant la même moyenne mais des écarts types différents illustrant l'écart type comme mesure de la dispersion autour de la moyenne.
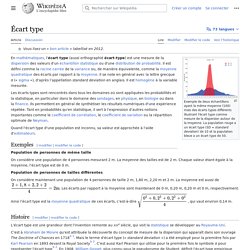
Histoire[modifier | modifier le code] L'écart type est une grandeur dont l'invention remonte au XIXe siècle, qui vit la statistique se développer au Royaume-Uni. Sur population totale[modifier | modifier le code] Définition[modifier | modifier le code] À partir d'un relevé exhaustif (x1, ..., xn) d'une variable quantitative pour tous les individus d'une population, l'écart type est la racine carrée de la variance, c'est-à-dire[b 3],[1] : [Note 1] L'écart type est homogène à la variable mesurée, c'est-à-dire que si par un changement d'unité, toutes les valeurs sont multipliées par un coefficient α > 0, l'écart type sera multiplié par le même coefficient.
Expression comme distance[modifier | modifier le code] , atteinte en son projeté orthogonal de coordonnées (x, ..., x). Corrélation (statistiques) En probabilités et en statistiques, étudier la corrélation entre deux ou plusieurs variables aléatoires ou statistiques numériques, c’est étudier l'intensité de la liaison qui peut exister entre ces variables.
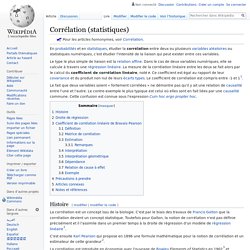
Le type le plus simple de liaison est la relation affine. Dans le cas de deux variables numériques, elle se calcule à travers une régression linéaire. La mesure de la corrélation linéaire entre les deux se fait alors par le calcul du coefficient de corrélation linéaire, noté r. Ce coefficient est égal au rapport de leur covariance et du produit non nul de leurs écarts types. En théorie des probabilités et en statistique, la covariance entre deux variables aléatoires est un nombre permettant de quantifier leurs écarts conjoints par rapport à leurs espérances respectives.
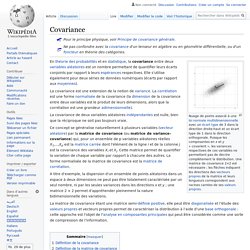
Elle s’utilise également pour deux séries de données numériques (écarts par rapport aux moyennes). À titre d'exemple, la dispersion d'un ensemble de points aléatoires dans un espace à deux dimensions ne peut pas être totalement caractérisée par un seul nombre, ni par les seules variances dans les directions x et y ; une matrice 2 × 2 permet d’appréhender pleinement la nature bidimensionnelle des variations. Définition de la covariance[modifier | modifier le code] La covariance de deux variables aléatoires réelles X et Y ayant chacune une variance (finie[1]), notée Cov(X, Y) ou parfois σXY, est la valeur : Définition — où désigne l'espérance mathématique. Covariance.