

Logic Gates. Gate types: NOT | AND | NAND | OR | NOR | EX-OR | EX-NORSymbols | Truth tables | Logic ICs | Summary truth tables | Combinations | Substituting Next Page: Capacitance and Uses of CapacitorsAlso see: Logic ICs | 4000 Series | 74 Series Introduction Logic gates process signals which represent true or false.

Normally the positive supply voltage +Vs represents true and 0V represents false. Other terms which are used for the true and false states are shown in the table on the right. Gates are identified by their function: NOT, AND, NAND, OR, NOR, EX-OR and EX-NOR. Digital logic functions : Ladder Logic - Electronics Textbook. We can construct simply logic functions for our hypothetical lamp circuit, using multiple contacts, and document these circuits quite easily and understandably with additional rungs to our original "ladder.
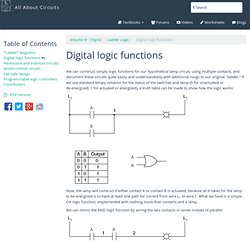
" If we use standard binary notation for the status of the switches and lamp (0 for unactuated or de-energized; 1 for actuated or energized), a truth table can be made to show how the logic works: Now, the lamp will come on if either contact A or contact B is actuated, because all it takes for the lamp to be energized is to have at least one path for current from wire L1 to wire 1. What we have is a simple OR logic function, implemented with nothing more than contacts and a lamp. We can mimic the AND logic function by wiring the two contacts in series instead of parallel: Now, the lamp energizes only if contact A and contact B are simultaneously actuated. Now, the lamp energizes if the contact is not actuated, and de-energizes when the contact is actuated. Logic: finding valid conclusions. Introduction This is not a general post about all methods of extracting valid conclusions, but I will be looking at more than just syllogistic reasoning.
I want to talk about the four logic questions I asked in my most recent happenings post. You may, but don’t need to, go back to that post… here are four pairs of premises. (And because we have two premises for each question, we may consider syllogistic reasoning, as well as other methods.) Boolean algebra (logic) From Wikipedia, the free encyclopedia Boolean algebra (or Boolean logic) is a logical calculus of truth values, developed by George Boole in the 1840s.
It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of conjunction x∧y, disjunction x∨y, and complement ¬x. The Boolean operations are these and all other operations that can be built from these, such as x∧(y∨z). These turn out to coincide with the set of all operations on the set {0,1} that take only finitely many arguments; there are 22n such operations when there are n arguments. Digital Logic - Using Minterms. Logic Functions Is It Important To Consider Better Methods?

Minterm Expansions Simplifying A Minterm Expansion Don't Care Terms Problems. Euler diagram. An Euler diagram illustrating that the set of "animals with four legs" is a subset of "animals", but the set of "minerals" is disjoint (has no members in common) with "animals" Venn and Euler diagrams were incorporated as part of instruction in set theory as part of the new math movement in the 1960s.
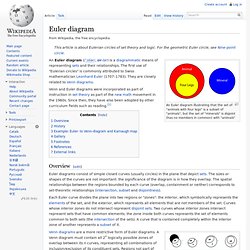
Since then, they have also been adopted by other curriculum fields such as reading.[1] Overview[edit] User:mate2code/Logic. Operations[edit] Relations[edit]
Euler Diagrams and Quantified Expressions. And finally the above figure on the right shows the diagram that corresponds to what your text refers to as the "Particular Negative," namely, the statement "Some A are not B.

" Again, the quantified statement that correspond to this case is shown at the bottom. Your text refers to these statements; "All A are B, "Some A are B, "No A are B, "Some A are not B," as 'categorical propositions.' And your text states on page 118 that "most of the propositions are ambiguous. " By this the author means that there is more than one Euler diagram that can be associated with the "categorical proposition. " But this presumes two things. Thus, in making sense of this chapter, it is useful to distinguish between an English statement, e.g., All A are B; the logical expression(s) that correspond to the English statement; and the semantic model(s) that correspond to the logical expression. The Geometry of Logic. Abstract: The phrase "algebra of logic" is commonly used to describe the classic work of Boole and others.

The phrase "geometry of logic" is less common; this note supplies some background on what it might mean. It is well known that the set of 16 connectives ("and," "or," etc.) of two-variable Boolean logic and the set of 16 subsets of an four-element set (a 4-set) have the same structure-- a Boolean lattice. It is also well known that the group of Boolean-lattice automorphisms, or symmetries, of the 16 connectives is isomorphic to the group of 24 permutations of the 4-set.
Nevertheless, some authors* have proposed additional automorphisms of the 16 connectives, based on symmetries of geometric figures (such as a Hasse diagram of the Boolean lattice) labeled by the connectives. All about Quine-McClusky. Using K-maps to simplify logic equations in hardware and software makes a lot of sense, but Quine-McClusky is more a systematic approach.

If you've been following this column for the last few months, you know that we've been talking about symbolic logic and the hardware circuits used to implement it. It wasn't really my intention to talk much about the hardware, since the focus of this column is on software tools. But I've noticed that most programmers don't know much about symbolic logic unless they've taken courses in digital circuitry. Since I believe that software can sometimes be simplified by using symbolic logic, I set out to teach the fundamentals.
One thing led to another, and the next thing I knew, I was describing how to build counters with J-K flip-flops. One doesn't have to wire up digital chips in order to learn and use symbolic logic. I think perhaps the best way to explain the value of logic minimization is by analogy to ordinary algebra. Equation 2. Existential Graphs. MS 514 by Charles Sanders Peirce with commentary by John F. Sowa Peirce wrote MS 514 in 1909 as a tutorial on existential graphs, their rules of inference, and related topics in logic. The original manuscript of MS 514 is located at the Houghton Library, Harvard University, and this version was transcribed by Michel Balat. Peirce’s words (either from MS 514 or in quotations from other sources) are printed in black, and the commentary is printed in red. Diagrams. 1. Introduction Diagrams or pictures probably rank among the oldest forms of human communication. They are not only used for representation but can also be used to carry out certain types of reasoning, and hence play a particular role in logic and mathematics.
However, sentential representation systems (e.g., first-order logic) have been dominant in the modern history of logic, while diagrams have largely been seen as only of marginal interest. Diagrams are usually adopted as a heuristic tool in exploring a proof, but not as part of a proof.[1] It is a quite recent movement among philosophers, logicians, cognitive scientists and computer scientists to focus on different types of representation systems, and much research has been focussed on diagrammatic representation systems in particular. We have the following goals for this entry. 2. The dominance of sentential representation systems in the history of modern logic has obscured several important facts about diagrammatic systems. 3. Syllogism. A syllogism (Greek: συλλογισμός – syllogismos – "conclusion," "inference") is a kind of logical argument in which one proposition (the conclusion) is inferred from two or more others (the premises) of a certain form.
In antiquity, there were two rival theories of the syllogism: Aristotelian syllogistic and Stoic syllogistic.[1] In the Prior Analytics, Aristotle defines the syllogism as "a discourse in which, certain things having been supposed, something different from the things supposed results of necessity because these things are so. " (24b18–20) Despite this very general definition, in the Prior Analytics, Aristotle limits himself to categorical syllogisms, which consist of three categorical propositions.[2] These included categorical modal syllogisms.[3] From the Middle Ages onwards, "categorical syllogism" and "syllogism" were mostly used interchangeably, and the present article is concerned with this traditional use of "syllogism" only.
Basic structure Conclusion: Some men die. Www.ee.calpoly.edu/media/uploads/resources/KarnaughExplorer_1.html. Digital Logic - Karnaugh Maps. Karnaugh Maps. From Wolfram MathWorld. In combinatorial logic minimization, a device known as a Karnaugh map is frequently used. It is similar to a truth table, but the various variables are represented along two axes and are arranged in such a way that only one input bit changes in going from one square to an adjacent square. It is also known as a Veitch diagram, K-map, or KV-map. The Karnaugh map may be used to quickly eliminate redundant operations in a Boolean function. Half-Truth Tables and Abnormal Forms. The Hitchhiker's Guide To Logic Old News Truth tableCNF/DNF, CCNF, CDNF.
Discrete Mathematics. A Boolean function or truth function f(x1, ..., xn) is a mapping f: { 0,1 }n {0,1}. It is completely determined by the corresponding truth table and vice versa. Convert Boolean Function to Boolean Expression Let B = { 0,1} and f: Bn B be a Boolean function. (i) List all possible input states and the corresponding function values, i.e. list the truths table. Begriffsschrift (Conceptual Notation)