

THE CENTER OF CURVATURE AND THE EVOLUTE. Ellipse. Definition of the Ellipse To read how the ellipse got its name, and what it means, see Parabola.

That page also contains some background information on conic sections and other topics that also applies to ellipses, that won't be repeated here. Finding the arc length of an ellipse, which introduces elliptic integrals, and Jacobian elliptic functions, are treated in their own articles. An oval is generally regarded as any ovum (egg)-shaped smooth, convex closed curve. Convex means that any chord connecting two points of the curve lies completely within the curve, and smooth means that the curvature does not change rapidly at any point.
Curvature. Arc Length Curvature Arc Length For a parametrically defined curve we had the definition of arc length.

Since vector valued functions are parametrically defined curves in disguise, we have the same definition. Osculating Circles for Plane Curves. Untitled. So, you want to more?
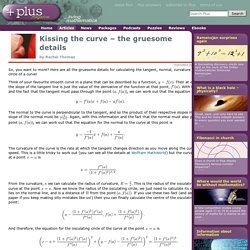
Here are all the gruesome details for calculating the tangent, normal, curvature and osculating circle of a curve! Think of your favourite smooth curve in a plane that can be described by a function, . Parametric Equation of an Ellipse. Scarpelli Assignment 10. Notice from the graphs above when a = b, the paramaterization of x and y is a circle centered at the origin (0,0) with radius equal to a.
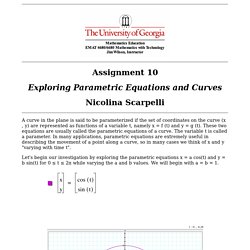
When a = b = 1, we have a graph of the unit circle. Since the domain of t is between 0 and 2π (approximately 6.28) or 360 degrees, the graph starts at t = 0, the point (a,0) or in this case (1,0), and moves in the counterclockwise direction around the origin to create a full circle that ends at t =2π, which is also the point (a,0) or in this case (1,0). The same holds for when a = b = 2 except the circle begins at t = 0, the point (2,0), and ends at t = 2π, also the point (2,0). To further investigate, hypothesize what will happen if your t - values range from 0 to π instead of 0 to 2π. How will your graph be different than the graph above? T hat, N hat, B hat and kappa. This figure shows T(0), N(0), and B(0).
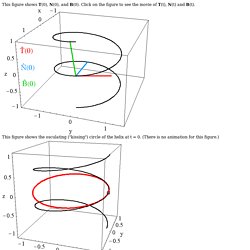
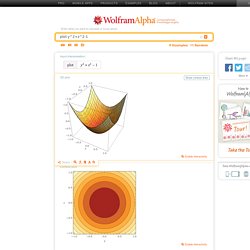
Click on the figure to see the movie of T(t), N(t) and B(t). This figure shows the osculating ("kissing") circle of the helix at t = 0. (There is no animation for this figure.) The ellipse x2/4 + y2/9 = 1 is shown in these figures. Combo. GraphSketch - Parametric. GraphSketch.com - Parametric Click here to download this graph.

Permanent link to this graph page. Mode: Functions Parametric Enter Graph Equations: Plot y^2+z^2-1. X Image InputX Upload an image from your computer: Enter a URL for an image: Terms | Privacy All images »Recent images Loading...
Sample images Data InputX Give numeric, tabular, or other data. Antiderivatives - Application Center. Antiderivatives Copyright Maplesoft, a division of Waterloo Maple Inc., 2007 Introduction This application is one of a collection of examples teaching Calculus with Maple.
These applications use Clickable Calculus methods to solve problems interactively. Steps are given at every stage of the solution, and many are illustrated using short video clips. Buttons to watch the videos. Problem Statement. Math Forum - Ask Dr. Math. Calculate the integral $\int_{0}^{2\pi}\frac{1}{a^{2}\cos^2t+b^{2}\sin^{2}t}dt$, by deformation theorem. Ellipse. Matematicas Visuales. From Wolfram MathWorld. An ellipse is a curve that is the locus of all points in the plane the sum of whose distances and from two fixed points (the foci) separated by a distance of is a given positive constant (Hilbert and Cohn-Vossen 1999, p. 2).
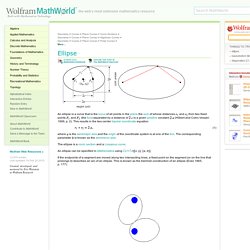
Where. Archimedes and the area of an ellipse: an intuitive approach. Algebra Conic Ellipse Equation Derivation. Study the following diagram for an ellipse: Recall the definition of an ellipse requires that d₁ + d₂ = 2a.
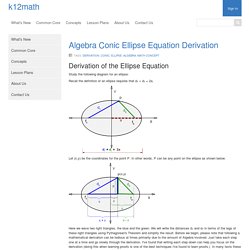
Let (x,y) be the coordinates for the point P. In other words, P can be any point on the ellipse as shown below. Here we wave two right triangles, the blue and the green. We will write the distances d₁ and d₂ in terms of the legs of these right triangles using Pythagorean's Theorem and simplify the result. D₁ + d₂ = 2a The general equation involves translation of coordinates from one coordinate system to another, that is moving from one origin to another. Conic Sections: Ellipse with Foci. Using Greens Theorem to find Area of an Ellipse. k12math - Algebra Conic Ellipse Equation Derivation. Using Green's theorem to find area - Math Insight. Typically we use Green's theorem as an alternative way to calculate a line integral \dlint.
If, for example, we are in two dimension, \dlc is a simpleclosed curve, and \dlvf(x,y) is defined everywhere inside \dlc, we can use Green's theorem to convert the line integral into to double integral. Instead of calculating line integral \dlint directly, we calculate the double integral \begin{align*} \iint_\dlr \left(\pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}\right) dA \end{align*} Can we use Green's theorem to go the other direction? If we are given a double integral, can we use Green's theorem to convert the double integral into a line integral and calculate the line integral?
If we are given the double integral \begin{align*} \iint_\dlr f(x,y) dA, \end{align*} we can use Green's theorem only if there happens to be a vector field \dlvf(x,y) so that \begin{align*} f(x,y) = \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}. Where \dlvf(x,y) = (-y/2,x/2). Area enclosed by an ellipse. Area enclosed by an ellipse From Latin: area - "level ground, an open space," The number of square units it takes to exactly fill the interior of an ellipse. Try this Drag the orange dots to move and resize the ellipse.
As the shape and size of the ellipse changes, the area is recalculated. An ellipse is actually a line, one that connects back to itself making a loop. Desmos Graphing Calculator. Desmos Graphing Calculator. Area between curves with multiple boundaries. Area between Curves. Area under a curve. How to calculate areas under a function graph. Theory: Area Under A Curve. Shading. Functions Domain Calculator - Symbolab. Domain of √(x + 2) / (x - 1) X Image InputX. Find Domain of a Function - Calculator. Composition of Functions - Domains. Visual Calculus - Drill - Domains of Functions. Calculus and algebra vs topology - Intelligent Perception. We revisit the subject of Topology via Calculus here but put it on a more solid, algebraic foundation. Once again, we start with dimension 1 and no forms. Suppose R is the union of m disjoint open intervals, I_1,...,I_m in {\bf R}.
Set-Builder Notation. How to describe a set by saying what properties its members have. Mathematics Calculus. What Is Domain and Range in a Function? - Video & Lesson Transcript. ActiveMath Applet: Arithmetic operations with real functions. Highschool Content of LeAM_calculus. Finding Domain and Range. Finding Domain and Range.